はじめに

こちらの本を読んでいます。

点過程の時系列解析 (統計学One Point)

作者:崇宏, 近江,俊一, 野村
発売日: 2019/06/08
メディア: 単行本

前半としてポアソン過程と更新過程の内容をまとめていました。

saltcooky.hatenablog.com

今回はホークス過程についての内容を簡単にまとめます。

ホークス過程

ホークス過程とは、あるイベントが発生した場合に、イベントが発生する強度が高く次のイベントを誘発してしまうような自己励起がある点過程である。

あるイベントが発生した時に、さらにイベントが群発する過程であるとも言える。

例えば、次のようなものがあげられる。

地震のように一度発生した場合に、その地震の影響により余震が発生する現象
金融市場において、ある大きな取引が行われることにより、多くの取引が発生する現象

ホークス過程の次のような条件付き強度関数により表現することができる。

$\displaystyle \lambda (t|H_t) = \mu + \alpha \sum_{ t_i < t } g(t-t_i)$

ここで $\mu＞0$ は定数であり、 $g(\tau)$ は過去のイベントからの影響を示すカーネル関数と呼ばれ、 $\tau \leq 0$ の時 $g(\tau)=0$ であり、 $\tau>0$ で非負である。

$\alpha$ は、過去のイベントからの影響の大きさを表現している。

例えば、イベント発生が以下のグラフの(a)のタイミングであった場合、強度関数の概形はグラフ(c)のようになる。

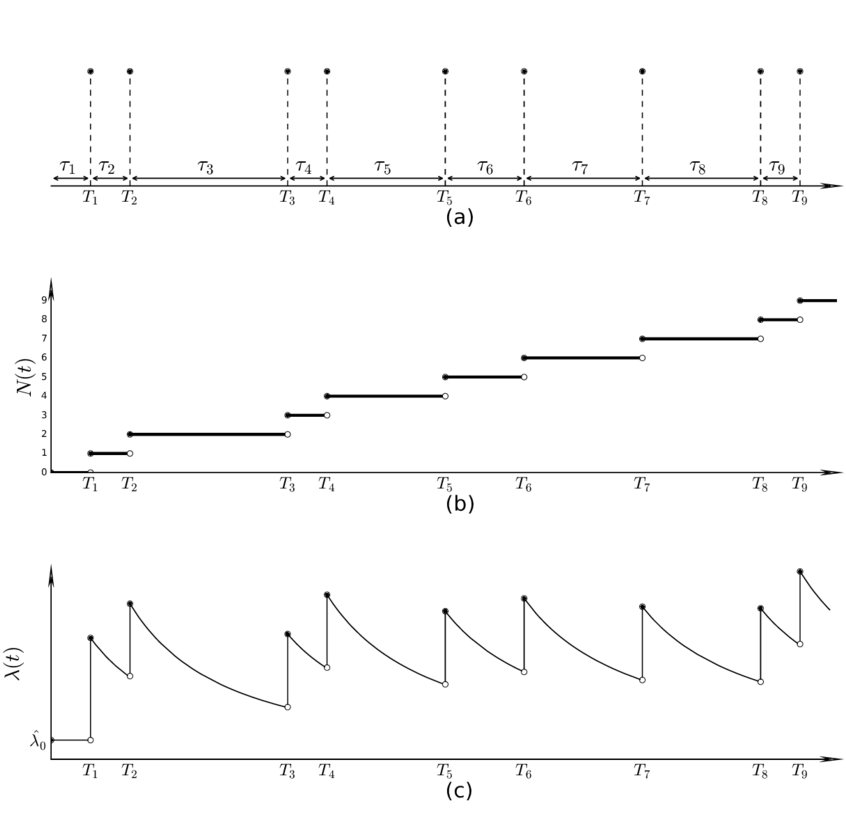
f:id:saltcooky:20210101233353p:plain

画像出典

この条件付き強度関数はベースラインとなるイベントが発生する確率 $\mu$ と過去のイベントからの影響を積み上げたものであるということを意味している。

カーネル関数には、次の指数関数やべき関数を用いることが多い。

$\displaystyle g(\tau) = a exp(-b\tau)$

$\displaystyle g(\tau) = \frac{K}{(\tau+c)^p}$

指数関数の場合、 $a$ はイベントが発生した時にそのイベントの発生により誘発される期待イベント数であるといえ、 $b$ はイベント発生確率の減衰の強さであると言えます。

確率密度関数

観測期間 $[0,T$ ]におけるホークス過程の確率密度間数は次のように表現できる。

$\displaystyle p_{[0,T]} (t_n) = \prod_{i=1}^n \left[ \mu + \sum_{j ＜ i} g(t-t_i) \right] × exp \left [ -\mu T - \sum_{i=1}^n \int_{t_i}^T g(s-t_i) ds \right ]$

この確率密度関数は陽に書き表せるが、第一項に総乗の中に総和があるため数値的に得るには大きな計算コストがかかることになる。

ホークス過程の定常性

ホークス過程が定常となる場合の平均強度関数は次のようになる。

$\displaystyle \lambda = E[\lambda (t|H_t)$ ]

この関係は次のように変形することができる。

$\displaystyle \lambda = \mu + \alpha \int_0^\infty g(\tau) d\tau = \mu + \alpha \gamma$

そして、平均強度は次のように表現できる。

$\displaystyle \gamma = \frac{\mu}{1-\alpha}$

この時、平均強度 $\lambda$ は非負であることが求められるため、ホークス過程が定常であるためには $\gamma$ <1であることが条件となる。

この値 $\gamma$ は、ホークス過程を特徴付ける値として分枝比(branching ratio)と呼ばれている。

カーネルに指数関数を用いた場合の、分枝比は次のようになる。

$\displaystyle \gamma = \int_0^\infty \alpha e^{-\beta t}dt = \frac{\alpha}{\beta}$

この分枝比が大きくなると一度イベントが発生すると続けてイベントが発生しやすくクラスターとなる可能性が高くなる。

一方で $\alpha \geq 1$ となる場合、イベント発生の連鎖が止まらずイベントが爆発的に発生することになる。

この時、平均発生率は時間と共に増加していくことになるため、定常性が成り立たなくなる。

イベント数の分布

観測期間が $[0,T$ ]ホークス過程のイベント数の分布を解析的に求めることは難しい。

しかし、観測期間が非常に長く極限をとるとする場合の全イベント数 $K_\infty$ の期待値と分散は次のように求めることができる。

$\displaystyle E[K_\infty ]=\frac{\mu T}{1-\gamma}$

$\displaystyle V[K_\infty ]=\frac{\mu T}{(1-\gamma)^3}$

期待値は期待値 $\mu T$ のポアソン分布に従うと言え、分散は分枝比 $\gamma$ が１に近くにつれ急激に大きくなることを意味している。

Rでホークス過程

Rでホークス過程を扱うには hawkes パッケージを使います。

はじめに、ホークス過程の時系列をシミュレーションします。

$\mu=0.2$ , $\alpha=0.7$ , $\beta=1.5$ と設定してみました。

なお、ここで分枝比の条件より $\alpha > \beta$ でないといけませんし、そのように設定していないとエラーが出てしまう設計になっているようです。

library(hawkes)
set.seed(1234)

N<-1440
lambda0 <- 0.02
alpha <- 0.7
beta <- 1.0
history <- simulateHawkes(lambda0, alpha, beta, N)

イベントタイミングを確認してみます。

f:id:saltcooky:20210211133549p:plain

累積イベント発生件数の推移も確認して見ます。

f:id:saltcooky:20210211133625p:plain

強度関数も確認してみます。

f:id:saltcooky:20210211133727p:plain

次に、過程のパラメータの推定を行っていきます。

このパッケージではモデル推定の関数は用意されていないませんが、尤度を算出する関数が存在しているため、パラメータの推定をoptim関数を用いて行います。

# ホークス過程の尤度計算用関数
cal_likelihood <- function(param, history){
  likelihoodHawkes(param[1], param[2], param[2]+param[3], history)
}

# パラメータの推定
params_hawkes <- optim(c(0.1,2,6),
                       cal_likelihood,
                       method = "L-BFGS-B",
                       lower = rep(0.000001,3),
                       upper = rep(10,3),
                       history = history[[1]],
                       control = list(maxit=10000))

推定結果を確認します。

> paste( c("mu", "alpha","beta"), round(c(res_hawkes$par[1:2],sum(res_hawkes$par[2:3])), 4), sep=" = ")

"mu = 0.0147"    "alpha = 0.8813" "beta = 1.0394"

概ね推定がうまくできていると考えれます。

観測期間の長さがある程度あれば推定はうまく行かないのでしょうか。

1440×5に観測時間を伸ばした場合の推定結果は次にようになりました。

> paste( c("mu", "alpha","beta"), round(c(res_hawkes$par[1:2],sum(res_hawkes$par[2:3])), 4), sep=" = ")
[1] "mu = 0.0199"    "alpha = 0.8132" "beta = 1.1568"

muの推定は精度良く行えるようになりましたが、alphaとbetaの推定は精度が良くなったとは言いにくいかもしれません。

多次元ホークス過程

ある過程のイベント発生が別の過程のイベントが発生するように、複数の点過程が相互に励起する作用がある過程を、多次元ホークス過程と呼ぶ。

ここでk番目の過程の条件付き強度関数は、次のように定義できます。

$\displaystyle \lambda_k(t|H_t) = \mu_k + \sum_{j=1}^K \alpha_{mj} \sum_{i:t_j^i < t} h_{mj}(t-t_i^j)$

ここで、 $mu_k$ はベースとなる励起の強さ、 $\alpha_{mj}$ を過程 $j$ から過程 $m$ への影響力の強さであり、非負の値をとります。

$\alpha_{mj}$ を行列で表現すると次のような重み付き隣接行列になる。

$\displaystyle A = \left[ \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1K} \\ a_{21} & a_{22} & \ldots & a_{2K} \\ \vdots & \vdots & \ddots & \vdots \\ a_{K1} & a_{K2} & \ldots & a_{KK} \end{array} \right ]$

$h_{mj}$ は、過程 $j$ から過程 $m$ への影響を考えるカーネル関数を表現している。

多次元ホークス過程では、過程間の因果性をモデル化していることになる。

多次元ホークス過程の定常性

１次元の場合と同様に定常状態の強度関数を考えると次のようになる。(以下変量は全てベクトル)

$\displaystyle \lambda = \mu + A \lambda$

これを変形して平均強度のベクトルの関係が得られる。

$\displaystyle \lambda = (I-A)^{-1}\mu$

ここから多次元ホークス過程が定常となるには、この関係が有限である必要がある。

このことから定常条件は、隣接行列 $A$ のスペクトル半径が1以下であることとなる。

Rで多次元ホークス過程

Rで多次元ホークス過程を扱うのも hawkes パッケージを使います。

2次元のホークス過程のシミュレーションを行います。

ベースとなる平均強度ベクトル $\mu$ の各要素はそれぞれ0.02、指数関数のカーネルのパラメータ $\beta$ は(0.4,0.5)、の隣接行列は次にように設定した。

$\displaystyle A = \left[ \begin{array}{cc} 0.3 & 0.02 \\ 0.02 & 0.4 \end{array} \right ]$

それでは実際に設定とシミュレーションを行います。

lambda0 <- c(0.02,0.02)
alpha <- matrix(c(0.3,0.02,0.02,0.4),byrow=TRUE,nrow=2)
beta <- c(0.4,0.5)
N <- 2000
history <- simulateHawkes(lambda0, alpha, beta, N)

シミュレーションにより得られた２つの系列を確認してみます。

f:id:saltcooky:20201231151514p:plain

次にoptim関数を用いてパラメータの推定を行います。

その前に、推定用の尤度を返す関数を定義します。

nloglik_multi_hawkes <- function(params, history, k){
  mu <- params[1:k]
  alpha <- matrix(params[(k+1):(k+k*k)],byrow=TRUE,nrow=2)
  beta <- params[(k+k*k+1):(k+k*k+k)]
  return(likelihoodHawkes(mu, alpha, beta, history))
}

パラメータの推定を行います。

res_hawkes <- optim(c(rep(0.01,2), rep(0.2,4),rep(1.0,2)),
                    nloglik_multi_hawkes, 
                       method = "L-BFGS-B",
                       lower = rep(0.000001,8),
                       upper = rep(10,8),
                       history = history,
                       k = 2,
                       control = list(maxit = 10000))

推定したパラメータを確認します。

params <- data.frame( estimates = res_hawkes$par)

rownames(params) <- c("mu_1", "mu_2", "alpha_11",
                      "alpha_12","alpha_21",
                      "alpha_22", "beta_1", "beta_2")

>params
          estimates
mu_1     0.02541579
mu_2     0.01655328
alpha_11 0.29647613
alpha_12 0.02979791
alpha_21 0.02042788
alpha_22 0.49278135
beta_1   0.37051372
beta_2   0.56710703

概ね設定通りの値が推定できたと考えられます。