はじめに
もしかしたら今の課題に使えるんじゃないかと思い調べてみました。
かなりのページ数なのでかいつまんでみています。
Difference in Differences
処置群に対し時間と共に処置状態に変化する場合の処置効果を推定する方法です。
置群の処置の前後で比較する場合に、季節トレンドや上昇トレンドなど時系列データ特有の特性により前後比較にはバイアスが発生してしまう。
そのため、対照群を用いて季節トレンドや上昇トレンドを表現することで、バイアスのない効果を推定することを目指している。
DIDは、ノンパラメトリックな方法とパラメトリックな方法がある。
パラメトリックな方法では、観測値のモデルを以下のように仮定する。
は個人
における個人効果、
は時刻
における時間効果、
は一定効果、
は介入の有無、
は因果効果を意味する。
以下の式に従い最小二乗法を用い各パラメータの推定を行う。
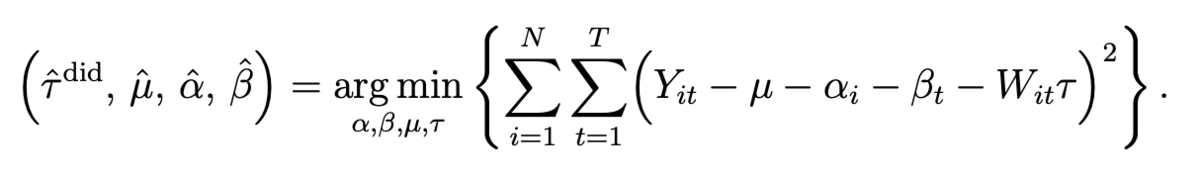
Synthetic Control
DIDは対照群の単純平均により介入のない場合の対照群を生成していますが、Synthetic Controlは対照群の加重平均で処置群を表現することにより、よりバイアスの少ない効果を推定する手法です。
対照群の動きを各対照群
の加重平均を用い近似する重みを
を考える。
![]()
この重みを用い処置が行われた時刻において処置を行わなかった場合の時系列を推定することで効果の推定を行う。
実際には、重み付きの最小二乗法を用い推定する。

に関するL2正則化項を導入して
の推定に安定性を持たせている。
Synthetic Difference in Differences
SCでは、時間方向/処置前後の変化や影響を加味していないため、バイアスが存在している。
そのため、Synthetic Difference in Differencesは、対象群をSCの考え方を用いて生成する際に時間方向の影響を取り入れることで、時間方向のバイアスを補正し因果効果を推定する方法である。
次のような二つの重みを加えた目的関数に従いパラメータを推定する。

ここで個体間につける重みで、対照群から処置群を予測するための重み。
は時間軸方向の重みで、非介入群において、介入前のデータから介入後のデータをうまく近似できるように、誤差最小化問題を解くことで算出されます。
検証
SCの論文で利用されていたカリフォルニアにおけるタバコ税の増税に関するデータを利用してSDIDの性能を検証している。
比較しているのは以下の五つ
SDID:synthetic difference in differences
SC:synthetic controls
DID:difference in differences
MC:matrix completion (2017年にAtheyらが提案した手法らしい)
DIFP:synthetic control with intercept

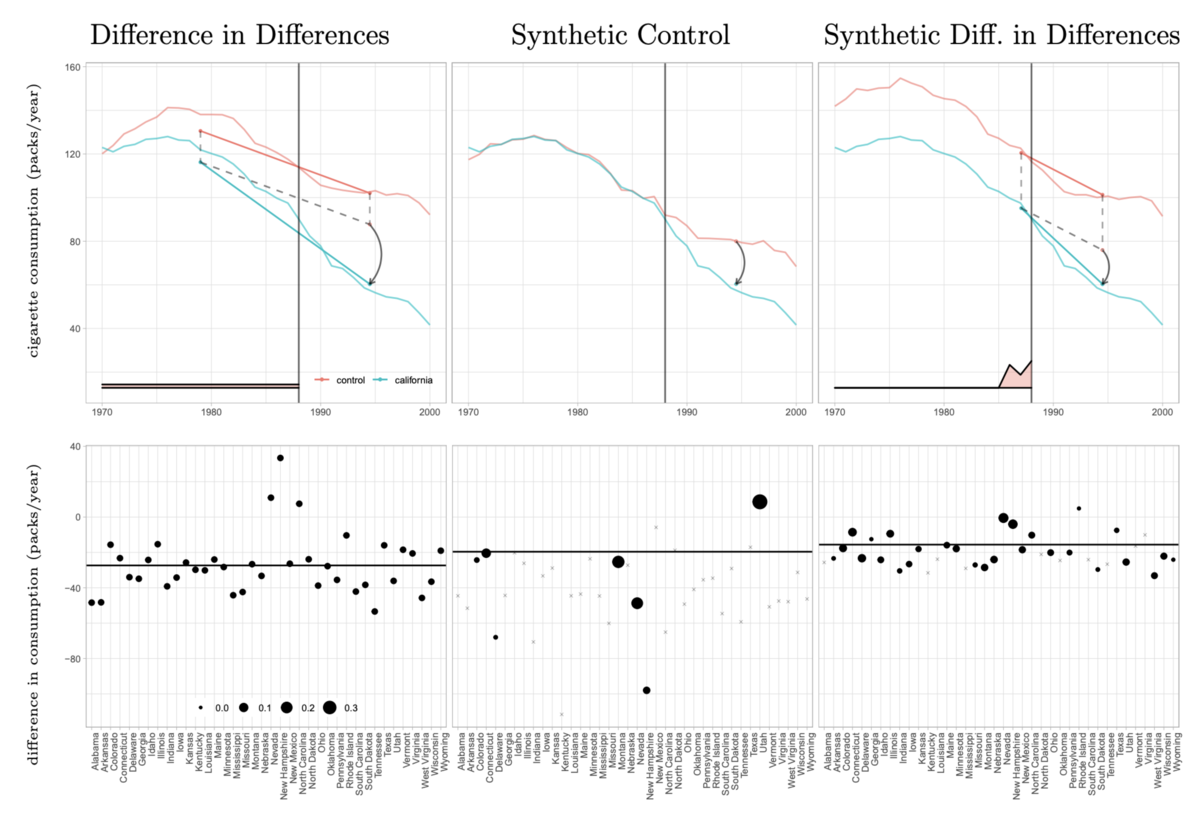
上が実測値と各手法の予測結果、下が各州の影響を意味する係数と重みを表現したもの。
SDIDはSCと比較すると係数が大きい州はなく、SCのように特定の州に推定値が引っ張られることなくなり過度な分散が発生しにくくなる。
これにより理想的な平行トレンド過程が満たせている状態に近づけれているらしい。
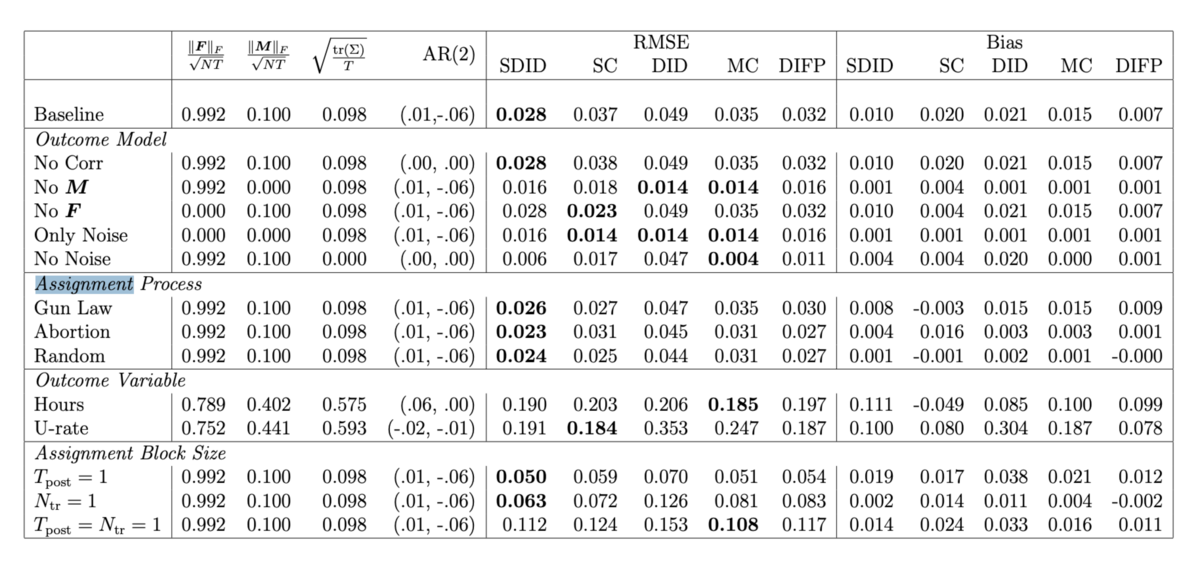
シミュレーションにより推定精度の確認も行なっている。
非常に簡単な(two-wayの固定効果/交互作用などを仮定しない)データ生成モデルでは、SCやDIDの方がRMSEが小さいが、それ以外の現実的な設定の場合はSDIDが最もRMSEが小さいことが多いそうです。
RでSynthetic Control
分析するデータとして以下のようなデータを生成しました
対象の10~15は120ステップ目以降から+300としています。
つまり推定したい因果効果が300となっています。


RでSynthetic Difference in Differences
RでSDIDを行うためにはgithubに上がっているsynthdidパッケージを利用します。
用意したサンプルデータをpanel.matrices関数を用いて、synthdidで扱える形式に変形する。
引数で与えるデータフレームにおけるunit, time, outcome, treatmentのカラム位置を指定する。
今回のデータフレームのカラムの並びはデフォルトの順番に対応しているのでそのまま関数に与えれば良い。
ts_treat_df <- read_csv("data/syndid_data.csv") %>% as.data.frame() setup_data <- ts_treat_df %>% dplyr::select(-target_no) %>% mutate(treat = as.integer(treat)) %>% panel.matrices()
このデータを用いモデルの推定を行う。
# modelfit estimate = synthdid_estimate(setup_data$Y, setup_data$N0, setup_data$T0) se = sqrt(vcov(estimate, method='placebo'))
推定された因果効果を確認すると、ほぼ設定通りの因果効果の推定が行えている。
> sprintf('point estimate: %1.2f', estimate) [1] "point estimate: 307.69"
合わせて95%信頼区間を確認すると、かなり信頼区間が広く統計的有意性は認められない。
> sprintf('95%% CI (%1.2f, %1.2f)', estimate - 1.96 * se, estimate + 1.96 * se) [1] "95% CI (-83.21, 698.59)"
推定されたモデルオブジェクトからグラフ描画すると以下のようになった。
plot(estimate)

比較のためにDIDとSCの場合でも推定を行いたいと思います。
synthdid パッケージではDIDとSCの推定が可能です。
DIDの推定には、did_estimateを用います。
didestimate = did_estimate(setup_data$Y, setup_data$N0, setup_data$T0) did_se = sqrt(vcov(didestimate, method='placebo'))
> sprintf('point estimate: %1.2f', didestimate) [1] "point estimate: 249.76" > sprintf('95%% CI (%1.2f, %1.2f)', didestimate - 1.96 * did_se, didestimate + 1.96 * did_se) [1] "95% CI (-385.49, 885.00)"

SCの推定にはsc_estimate関数を用います。
# SC modelfit scestimate = sc_estimate(setup_data$Y, setup_data$N0, setup_data$T0) sc_se = sqrt(vcov(scestimate, method='placebo'))
> sprintf('point estimate: %1.2f', scestimate) [1] "point estimate: 271.31" > sprintf('95%% CI (%1.2f, %1.2f)', scestimate - 1.96 * sc_se, scestimate + 1.96 * sc_se) [1] "95% CI (-115.96, 658.57)"
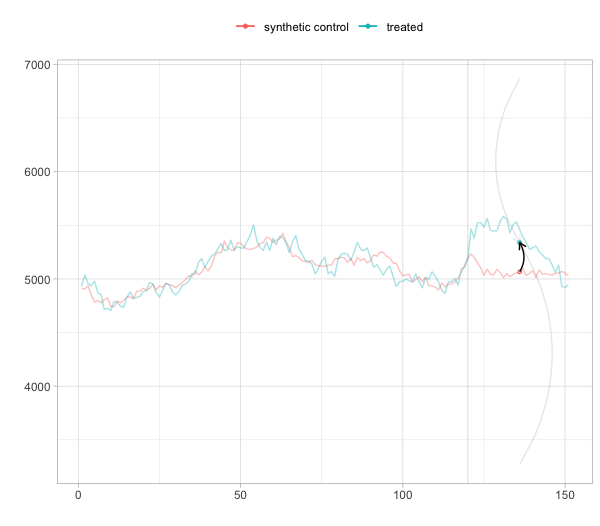
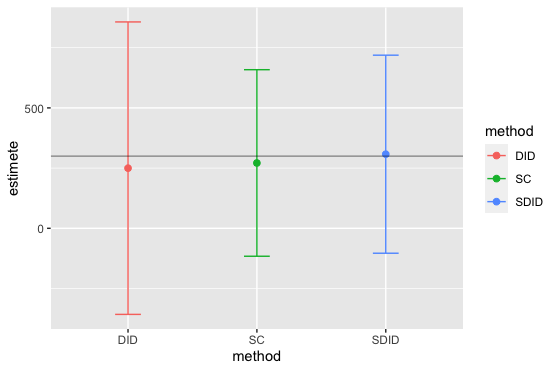
結果をまとめると以下のようになりました。
SDIDが期待値が最も誤差が少ないですが、SCの方が信頼区間の幅が小さいようです。
データ生成メカニズムの過程が比較的単純であったからかもしれません。