はじめに

気になっていたこちらの書籍を読みました。

非線形時系列解析の基礎理論

作者:平田祥人,陳洛南,合原一幸
東京大学出版会

Amazon

元々学生の時に少し齧った内容だったので、非常に楽しかったです。

12章仕立てで様々な話題を広く薄く扱っており、読みやすかったです。

しかし、終盤の応用系の話がかなりさらっとしているのは、残念でした。

とわ言え面白い内容だったので、基本的なところをまとめておきます。

時系列データのカオス性

この書籍では非線形な時系列データを力学系理論を用いて解説している。

力学系(dynamical systems)では、現在や過去の状態からその将来の状態が決まるシステムのことです。

単純なルールで将来の状態が決まるのに複雑な振る舞いが現れるのが特徴。

これを代表例が決定論的カオスであり、典型例としてエノン写像があげられる。

エノン写像は次の式で定義される。

$\displaystyle{ \begin{align} x_t=1-\alpha x_{t-1}^{2}+\beta x_{t-2} \end{align} }$

ここで、 $\alpha$ と $\beta$ は実パラメータであり、よく用いられるのは $\alpha=1.4$ と $\beta=0.3$ である。

DChaos packageを利用して、エノン写像の時系列を生成する。

library(DChaos)
N <- 500
ts <- henon.sim(a=1.4, b=0.3, s=0, n=N)

また、このエノン写像をリターンプロットと呼ばれるt時点とt+1時点の値のペアをプロットしたグラフも示す。

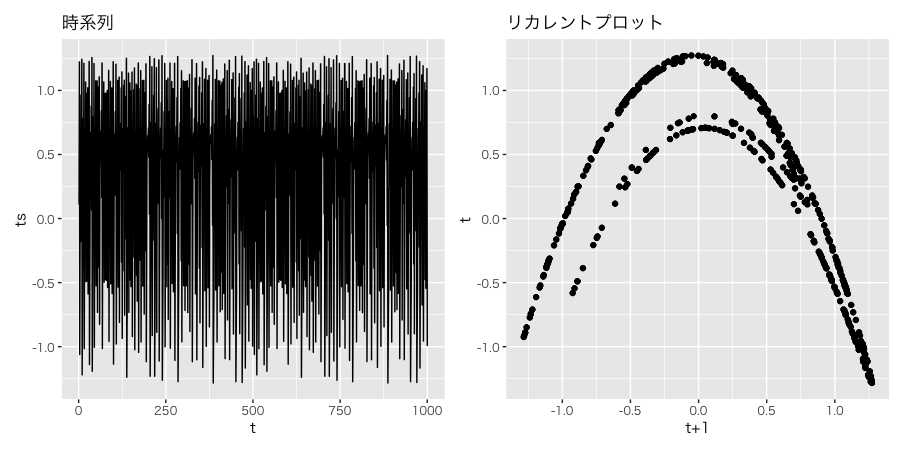
すると特定の部分にのみ点がプロットされる。この特定の点の集まりをアトラクタと呼ぶ。

ランダムな時系列の場合は、アトラクタは存在しない。カオス性を持つ時系列の代表例は他に、ロジスティック写像とガウス写像がある。

ロジスティック写像

$\displaystyle{ \begin{align} x_t=\alpha x_{t-1}(1-x_{t-1}) \end{align} }$

# ロジスティック写像
ts <- logistic.sim(n=N, a=4, s=0)

ガウス写像

# ガウス写像
ts <- gauss.sim(alpha=6.2, beta=-0.5, s=0, n=N)

また、ローレンツモデルと呼ばれる3変数常微分方程式で定義されるモデルもある。

$\displaystyle{ \begin{align} \frac{dx}{dt} &= - \sigma (x-y) \\ \frac{dy}{dt} &= -xz + rx-y \\ \frac{dz}{dt} &= xy -bz \\ \end{align} }$

パラメータを $\sigma = 10$ , $r = 28$ , $b = 8/3$ とし、初期値を $X = 0$ , $Y = 1$ , $Z = 1$ とした時系列データとアトラクタは次のようになる。

初期値鋭敏性

カオス性を持つ時系列は、初期値が少し変化しただけで、その後の時間経過があると大きく異なる軌道を示すことが知られている。

これを初期値鋭敏性やバタフライ効果と呼ぶ。

自己相似構造

アトラクタには、一部を拡大すると全体の構造と類似の幾何学的構造が見られる。

このような、構造があることを自己相関構造やフラクタル性があると言う

時系列データのカオス性指標

時系列のカオス性を測る指標の代表例として相関次元と最大リャプノフ指数が挙げられる。

相関次元

相関次元とは、距離rのよりも小さな2つの点の対の数が $r ^ D$ に比例しているとき、 $D$ が相関次元となる。

相関和と呼ばれる、時系列の相関性を表現する統計量が次のように定義される。

$\displaystyle{ \begin{align} C(r) = \frac{1}{T^2} \sum_{i,j=1}^T \theta (r - || v_i -v_j||) \end{align} }$

ここで $\theta (x)$ は、 $x$ が0以上なら1、そうでないなら0を取るヘビサイド関数と呼ばれる関数である。

$r$ が十分小さいところで次の関係が成り立つ。

$\displaystyle{ \begin{align} C(r) \propto r^D \end{align} }$

$C(r)$ の対数を取ると $r$ が十分小さいところで次のようになる。

$\displaystyle{ \begin{align} log C(r) = c_0 +D log r \end{align} }$

この時のDが相関次元となる。

例としてエノン写像における相関次元を求める。

nonlinearTseries packageを利用する。

N=2000
ts <- henon.sim(a=1.4, b=0.3, s=0, n=N)

cd = corrDim(time.series=as.numeric(ts),
             min.embedding.dim=2,
             max.embedding.dim=5,
             time.lag=10,
             min.radius=1e-3,
             max.radius=50,
             n.points.radius=100,
             theiler.window=100,
             number.boxes=100,
             do.plot=F)

plot(cd, type="l")
estimate(cd, regression.range=c(0.01,1))
# 1.804719

相関次元を推定するために必要な時系列データの長さは次のようにもとまる。

$\displaystyle{ \begin{align} N \ge 10^{frac{D}{2}} \end{align} }$

最大リャプノフ指数

最大リャプノフ指数は、2つの近傍点を初期条件とする2つの軌道が、時間経過とともにどのぐらいの速さで指数関数的に離れていくかを示す量。

初期値鋭敏性の評価に利用することができる。

決定論的カオスである場合、tステップ後の2点間の距離は、一般的に指数関数的に大きくなっていく性質がある。

係数 $k$ を用いると、次のように変化していくと考えられる。

$\displaystyle{ \begin{align} \sigma _t = || v_{i+t} - v_{i_j+t}|| \approx 2^{kt}\sigma_0 = 2^{kt} || v_{i} - v_{i_j}|| \end{align} }$

これの対数を取ると次のようになる。

$\displaystyle{ \begin{align} log_2 || v_{i+t} - v_{i_j+t}|| \approx log_2 \sigma_0 +kt \end{align} }$

左辺は時間tに対して線形に増加している。 iに関して平均をとる。

$\displaystyle{ \begin{align} < log_2 || v_{i+t} - v_{i_j+t} || >_ {i,j} \end{align} }$

最大リャプノフ指数は、これをtの関数としてプロットして、その傾きを求めることで得られる。

例として、エノン写像の最大リャプノフ指数を推定する。

RではnonlinearTseries packageを用いる。

library(nonlinearTseries)

ts = as.numeric(henon.sim(a=1.4, b=0.3, s=0, n=5000))
estimation = maxLyapunov(time.series = ts,
                         embedding.dim = 2,
                         time.lag = 1,
                         radius = 0.001,
                         theiler.window = 4, 
                         min.neighs = 2, 
                         min.ref.points = 500,
                         min.time.steps = 5,
                         max.time.steps = 20)
estimate(estimation)

# [1] 0.3617881