はじめに

共立出版のOne point シリーズの野村俊一(著)「カルマンフィルタ」を読みました。

カルマンフィルタ ―Rを使った時系列予測と状態空間モデル― (統計学One Point 2)

作者:野村俊一
発売日: 2016/09/08
メディア: 単行本

最後に粒子フィルタに触れています。

昔に、岩波データサイエンスVol.6で概要だけ知っている状態だったため、簡単にまとめてみました。

非線形非ガウス状態空間モデル

一般的な状態空間モデルは次にように表現される。

$\displaystyle{\begin{eqnarray} y_t & \sim & h_t(y_t|\alpha_t) \\ \alpha_(t+1) & \sim & q_t(\alpha_{(t+1)}|\alpha_t), t=1,\dots,n \\ \alpha_1 & \sim & p(\alpha_1) \tag{1} \end{eqnarray} }$

上から順に、状態 $\alpha_t$ に依存して観測値 $y_t$ が生成される観測モデル、状態 $\alpha_t$ から状態 $\alpha_{t+1}$ の遷移を表現したシステムモデル、初期状態分布を構成する式である。

ここで、各時点 $t=1,\dots , n$ の $h_t(y_t|\alpha_1)$ および $t=1,\dots , n$ の $q_t(\alpha_{t-1}|\alpha_1)$ は条件付き確率密度関数あるいは条件付き確率関数, $p(\alpha_1)$ は初期状態の周辺確率密度関数である。

観測モデルに関して、同時点の状態 $p(\alpha_1)$ を与えれば、それ以前の状態と観測値は依存しない。

$\displaystyle{\begin{eqnarray} p(y_t|\alpha_1,\dots,\alpha_t, Y_{t-1} ) = p(y_t|\alpha_t)=h_t(y_t|\alpha_t) \end{eqnarray} }$

また、システムモデルでも、同時点の状態 $p(\alpha_1)$ を与えれば、それ以前の状態と観測値は依存しない。

$\displaystyle{\begin{eqnarray} p(\alpha_t|\alpha_1,\dots,\alpha_t, Y_{t-1} ) = p(\alpha_{t+1}|\alpha_t)=q_t(\alpha_{t+1}|\alpha_t) \end{eqnarray} }$

上記の性質は時系列モデルにおけるマルコフ性と呼ばれている。

線形ガウスモデルの状態空間モデルに対する処理は、推定する状態や予測値の条件付き分布が全て正規分布であったため、条件付き平均と条件付き分散を推定できればよかった。

しかし、非ガウスモデルでは、条件付き分布の特定には確率関数の推定が必要になる。

以下で示す漸化式は確率密度関数を逐次計算するものとなる。

フィルタリング漸化式

各時点における、フィルタ化密度 $p(\alpha_t|Y_i)$ と状態と観測値の１期先予測密度 $p ( \alpha_{ t+1 } | Y_i )$ , $p ( Y_{ t+1 } |Y_i )$ は、以下の漸化式1~3を順に繰り返すことで得られる。

観測値の１期先密度関数 $p(y_t|Y_i)$ を用いてフィルタ化密度 $p(\alpha_t|Y_i)$

$\displaystyle{\begin{eqnarray} p(\alpha_t| Y_t ) = \frac{h_t(y_t|\alpha_t) p(\alpha_t|Y_{t-1})}{p(y_t|Y_{t-1})} \end{eqnarray} }$

フィルタ化密度から状態の１期先予測密度の算出

$\displaystyle{\begin{eqnarray} p(\alpha_{t+1}| Y_t ) = \int q_t(\alpha_{t+1}|\alpha_t) p(\alpha_t|Y_{t}) d \alpha_t \end{eqnarray} }$

状態の1期先予測密度から観測値の1期先予測密度を算出

$\displaystyle{\begin{eqnarray} p(y_{t+1}| Y_t ) = \int h_{t+1}(y{t+1}|\alpha_{t+1}) p(\alpha_{t+1}|Y_{t}) d \alpha_t \end{eqnarray} }$

状態平滑化漸化式

先に示したフィルタリング漸化式の結果を用いて観測値 $y=Y_n$ が与えられたもとでの状態 $\alpha_t$ の状態平滑化密度 $p(\alpha_t|y)$ をえる。

$\displaystyle{\begin{eqnarray} p(\alpha_t| y ) = p(\alpha_t| Y_t ) \int \frac{q_t(\alpha_{t+1}|\alpha_t)}{ p(\alpha_{t+1}|Y_t)} p(\alpha_{t+1}|y) d \alpha_{t+1} \end{eqnarray} }$

予測漸化式

$j=1,2,\dots$ について、状態の $j$ 期先の予測密度 $p (\alpha_{ n+j } | y )$ と、観測値の $j$ 期先の予測密度 $p ( y _{ n+j } | y )$ は、以下の漸化式1と2を $j=1,2,\dots$ の順に繰り返すことで得られる。

状態の $j-1$ 期先の予測密度から状態の $j$ 期先の予測密度を算出

$\displaystyle{\begin{eqnarray} p(\alpha_t| y ) = \int q_{n+j-1}(\alpha_{n+j}|\alpha_{n+j-1}) p(\alpha_{n+j-1}|y) d \alpha_{n+j-1} \end{eqnarray} }$

2.状態の $j-1$ 期先の予測密度から観測値の $j$ 期先の予測密度を算出

$\displaystyle{\begin{eqnarray} p(y_{n+j}| y ) = \int h_{n+j}(y_{n+j}|\alpha_{n+j}) p(\alpha_{n+j}|y) d \alpha_{n+j-1} \end{eqnarray} }$

粒子フィルタ

ここまでの漸化式は非線形非ガウス状態空間モデルにおいて、積分計算が解析的に不可能である。

そのため、非線形非ガウス状態空間モデルでは粒子フィルタと呼ばれるフィルタリング手法を用いる。

粒子フィルタによるフィルタリング

$t=1,...,n$ の順に、一時点前 $t-1$ のフィルタ化分布からのサンプル $\alpha _{t-1}^{(i)}, \dots , \alpha _{t-1}^{(N)}$ を元に、時刻 $t$ のフィルタ化分布からのサンプル $\alpha _{t}^{(i)}, \dots , \alpha _{t}^{(N)}$ を以下の1~3の手順を繰り返し得る操作を取る。

なお、観測値が欠損している場合は手順2,3をスキップする。

1.１期先予測サンプリング $i=1,2,\dots,N$ において、前時点 $t-1$ の状態を $\alpha _{t-1} = \alpha _{t-1}^{(i)}$ とおいた時の１期先予測分布 $q_{t-1} ( \alpha _t | \alpha _{t-1} ^{(i)})$ からサンプルを一つ抽出して $\tilde{\alpha} _{t-1}$ とおく。

尤度による重み付け $i=1,2,\dots,N$ において、観測値 $y_t$ に対する尤度 $w _t ^{(i)} = h_t ( y_t | \tilde{\alpha} _{t} ^{(i)})$ を、サンプル $\tilde{\alpha} _{t-1}$ に対する重みをする。
サンプリングサンプルとその重みから、次のインポータンスサンプリングを行い、重複を許したN個の状態サンプルを抽出する

3-1.割り当て関数の作成 $k=1,2,\dots,N$ に対して累積相対重みを次のように定義する。

$\displaystyle{\begin{eqnarray} W_t^(k) = \frac{ \sum_{i=1}^k w_t^{(i)}}{\sum_{i=1}^N w_t^{(i)}} \end{eqnarray} }$

そこから $0\leq r \leq 1$ に対する割り当て関数 $A(r)$ を次にように定義する。

$\displaystyle{\begin{eqnarray} A(r) =min \{ k | r \leq W_t^{(k)}\} \end{eqnarray} }$

3-2.層化サンプリング区間(0,1)上の一様分布からの１つのサンプル $u$ を抽出し、 $u$ の値に基づいて $u$ から次のようにリサンプリングを行う

$\displaystyle{\begin{eqnarray} \alpha_t ^ {(i)} = \tilde{ \alpha } _t ^{ A [ (i-1+u) / N ] } , ~~ i=1,\dots,N. \end{eqnarray} }$

これは、尤度の低い外れ値のようなサンプルを高確率で除き、尤度の高いサンプルを重視することを意味する操作である。

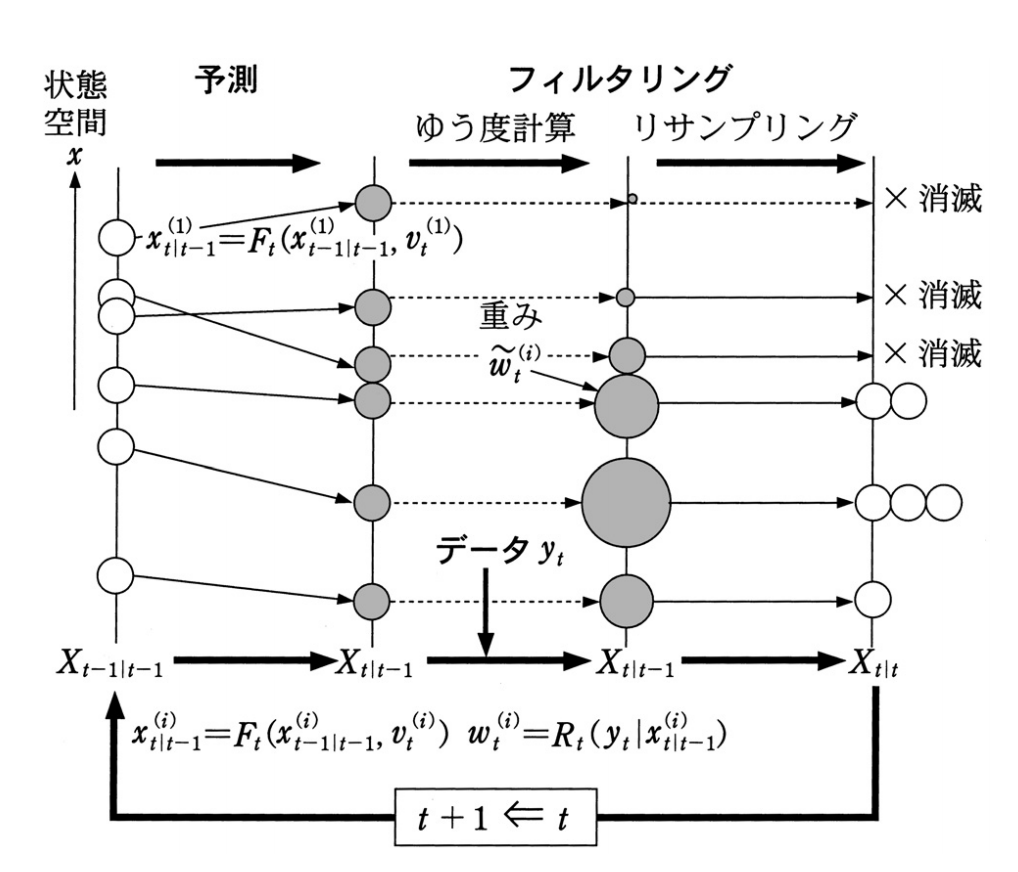
図で示すと次にようになる。

f:id:saltcooky:20200808153054p:plain 出典

粒子フィルタによる状態平滑化

粒子フィルタの結果からでは平滑化することができない。

そのために、固定ラグ平滑化という方法が提案されている。

観測値 $Y_t$ が得られたもとでのL時点前の状態を条件付き分布 $p( \alpha _ { t-L } | Y_t )$ からサンプリングを行うことで、平滑化状態分布 $p( \alpha_{t-L}|y_t)$ からの近似サンプルとして利用する方法である。

固定ラグ平滑化では、時点 $t$ の状態 $\alpha_t$ に対して、 $L$ 時点前までの状態 $\alpha _ {t-1|t}, \dots , \alpha _ {t-L|t}$ を結合した、拡大した状態ベクトル $\alpha_t =(\alpha' _ {t|t} , \alpha' _ {t-1|t}, \dots , \alpha' _ {t-L|t})$ に対して粒子フィルタを実行する。

具体的には粒子フィルタの手順1を次のように行う。

1'. 前時点の状態サンプル $\alpha _ t ^{(i)} = ( \alpha _ {t-1|t-1} ^{(i)'}, \dots , \alpha _{ t-L-1 | t-1 } ^{(i)'} )'$ の最初の要素を用いた１期先予測分布 $q _ {t-1}(\alpha_t | \alpha _ {t-1|t-1} ^{(i)})$ からサンプルを一つ抽出して $\tilde \alpha _ {t|t} ^{(t)}$ とおく。

それを前時点の状態サンプルと結合して $\alpha _ t ^{(i)} = ( \tilde \alpha _ {t|t} ^{(i)'}, \alpha _ {t-1|t-1} ^{(i)'}, \dots , \alpha _{ t-L-1 | t-1 } ^{(i)'} )'$ とおく。

そして、2以降の手順をフィルタリングの時と同様に行う。

現在の尤度を用いて過去の状態に対してサンプリングを適用することを繰り返すことになる。

これにより、時刻L先までの状態の尤度が高くなるように多くのサンプルが消滅することになる。

粒子フィルタによる状態予測

$j$ 期先予測は、１期先予測サンプリングを $t=n+j$ までを繰り返すことで可能である。

Rで粒子フィルタ

こちらの記事に掲載されているコードを参考にさせてもらいました。

chiral.hatenablog.com

ぞれぞれの関数を次にように作成しました。

# 尤度計算
likelihoods = function(xt,yt) {
  return(exp(-(yt-xt)**2))
}

# リサンプリングを行う関数
resampling <- function(x,w) {
  # input dim(x) = (N*M,D)
  # --> output dim = (D,N)
  N <- length(x)
  wsum <- c()
  
  for (i in 1:N) {
    wsum <- c(wsum,sum(w[1:i]))
  }
  
  
  total <- sum(w)
  pos <- (1:N) * total/N
  r <- runif(1,0,total) # roulette
  pos <- (pos+r) %% total
  point <- c()
  
  for (i in 1:N) {
    j <- which(wsum>=pos[i])[1]
    point <- append(point,j)
  }
  
  return(point)
}

fixedlag_smooth <- function(X, XX, t, point, width){
  for (w in 1:(width-1)) {
    tmp <- t-(width-w)
    if(tmp<1){ tmp <- 1 }
    #message(tmp)
    XX[[tmp]] <- XX[[tmp]][point]
  }
  XX[[t]] <-X[point]
  return(XX)
}


# フィルタリングを行う関数
particle_filter <- function(y, x0, N, sys.nois) {
  tmax <- length(y)
  D <- length(x0) # == ncol(y)
  xx <- list(rep(x0,N))

  for (t in 1:tmax) {
    #message(t)
    x <- xx[[t]] + rnorm(N, 0, sys.nois)  
    w <- likelihoods(x, y[t])  
    sp <- resampling(x, w) 
    xx[[t+1]] <- x[sp]
  }
  return(xx)
}

# スムージングを行う関数
particle_smoother <- function(y, x0, N, L, sys.nois) {
  tmax <- length(y)
  D <- length(x0) # == ncol(y)
  xx <- list(rep(x0,N))

  for (t in 1:tmax) {
    #message(t)
    x <- xx[[t]] + rnorm(N, 0, sys.nois) #t+1の状態のサンプリング(予測)
    w <- likelihoods(x, y[t]) # 尤度の計算
    sp <- resampling(x, w) # リサンプリングでインデックス取得
    xx <- fixedlag_smooth(x, xx, t, sp, L) # 
    xx[[t+1]] <- xx[[t]] 
  }
  
  return(xx)
}

今回適用したデータは岩波データサイエンスVol.6で用いられているデータをサポートページから持ってきました。

真の状態の変化と観測値を確認してみます。

時刻20付近で大きくトレンドがシフトしています。その後、緩やかにトレンドがドリフトしていることを確認できます。

f:id:saltcooky:20200811000237p:plain

上記で定義した関数を用いて、フィルタリングを行ってみました。

resFil <- particle_filter(y = dat$y, x0 = -0.5, N = 5000, sys.nois = 0.2)

f:id:saltcooky:20200810234720p:plain

そして、上記で定義した関数を用いて、スムージングを行ってみました。

resSm <- particle_smoother(y = dat$y, x0 = -0.5, N = 5000, L = 20, sys.nois = 0.2)

f:id:saltcooky:20200810234703p:plain

いい感じに滑らかになっていると思います。

書籍の一番最後に乗っていた金利の変化のCIRモデルを実装したかったですが、とりあえず、ここで一旦終わります。

名前はまだない

データ分析とかの備忘録か, 趣味の話か, はたまた

粒子フィルターと粒子スムージングについて簡単に