はじめに

情報量基準の復讐も兼ねて簡単にまとめます。

こちらの内容をまとめたものです。

社会科学のためのベイズ統計モデリング (統計ライブラリー　)

作者:浜田宏,石田淳,清水裕士
発売日: 2019/12/01
メディア: 単行本（ソフトカバー）

事前設定

ある確率モデルとデータから得られた予測分布 $p*(x)$ と真の分布 $q(x)$ との違いを表現する交差エントロピーをはんか誤差とよび、次のように定義され変形される

$\displaystyle{ G_n = - E_{p( \theta | x_n)} [ log p^*(X) ] \\ = -\int log p^*(x) q(x)dx \\ = H(q) + D(q||p^*) }$

また経験損失を予測分布から次にように計算することができる。

$\displaystyle{ T_n = G_n = - \frac{1}{n} \sum_{i=1}^n log p*(x_i) }$

AIC

AICを検討する際に次の要素を仮定する

真の分布は想定される確率モデルの中に含まれる
サンプルはi.i.d
$q(x)$ は確率モデルについて正則である

最尤推定値をもとにした予測分布は次にようになります。

$\displaystyle{ p^*(x) = p(x|\hat \theta) }$

この時の汎化誤差は平均対数尤度の符号を反転させたものに一致する。

$\displaystyle{ G_n = - E_{q(X)} [ log p^*(X) ] \\ = - E_{q(X)} [ log p^*(X|\hat \theta) ] \\ = -\int log p^*(x|\hat \theta) q(x)dx }$

これは予測の良さを表現すると言える。

一方、経験損失は次のように最大対数尤度の $-1/n$ 倍したものと算出できる。

$\displaystyle{ T_n = - \frac{1}{n} \sum_{i=1}^n log p(x_i | \hat \theta) }$

ここで、予測分布の導出に利用したデータと同じデータで経験損失を算出しており、そこにはバイアスが存在している。

データ $x ^ n$ の元でのバイアスは次のようになる。

$\displaystyle{ b(x^n) = G_n -T_n = -E_{q(X)} [ log p(X|\hat \theta) ] + \frac{1}{n} \sum_{i=1}^n log p(x^n | \hat \theta) }$

もし、新たに予測する確率変数 $Z$ とするデータを与えられた時、偏りの期待値は次のように表現できる。

$\displaystyle{ E_{q(X^n)} [ b(x^n) ] = E_{q(X^n)} [ G_n -T_n ]= E_{q(X^n)} [ -E_{q(X^n)} [ log p(Z|\hat \theta) ] + \frac{1}{n} \sum_{i=1}^n log p(x^n | \hat \theta) ] }$

この二つの損失のバイアスの期待値は、真の分布は想定される確率モデルの中に含まれるという仮定の元で、漸近的に $d/n$ に従うことが知られている。このことからAICは次のように定義される。

$\displaystyle{ AIC = T_n + \frac{d}{n}= - \frac{1}{n} \sum_{i=1}^n log p(x_i | \hat \theta) + \frac{d}{n} }$

詳細は、北川の3.4に記載されている。

WAIC

WAICではベイズモデルにおける汎化損失の推定を考えていきます。

このときに、以下を仮定しています。

真の分布は想定される確率モデルの中に含まれなくて良い
サンプルはi.i.d
$q(x)$ は確率モデルについて必ずしも正則でなくても仮定

ベイズ推定により得られた予測分布は確率モデルを事後分布により、次のように得られる。

$\displaystyle{ p^*(x) = E_{p( \theta | x_n)} [ p(x | \theta) ] = \int p(x | \theta)p( \theta|x_n) d \theta }$

ベイズ予測分布の汎化損失 $G_n$ は次のようになります。

$\displaystyle{ G_n = - E_{q(X)} [ log p^*(X) ] \\ = - E_{q(X)} [ log p^*(X|\hat \theta) ] \\ = -\int \int q(x) \left( log p^*(x| \theta) p^*( \theta | x^n) d\theta \right) dx }$

次に経験損失 $T_n$ は、次のようになる。

$\displaystyle{ T_n = - \frac{1}{n} \sum_{i=1}^n log E [ p(x_i | \theta) ] }$

AICと同様に二種類の損失にはバイアスが生じると考えられ、その期待値は次のようにある。

$\displaystyle{ E_{q(X^n)} [ b(x^n) ] = E _{q(X^n)} [ G_n -T_n ] }$

このバイアスは漸近的に次の汎関数分散 $V_n$ を $n$ で割った値に一致することが知られている。

$\displaystyle{ V_n = \sum_{i=1}^n \{ E_{p(\theta | x^n)} [(log p(x_i | \theta))^2 ] - E_{p(\theta | x^n)} [log p(x_i|\theta) ]^2 \} }$

WAICは経験損失と汎関数分布を $n$ で割った値の和として定義される。

$\displaystyle{ WAIC = T_n + \frac{V_n}{n} \\ = - \frac{1}{n} \sum_{i=1}^n log E [ p(x_i | \theta) ] + \sum_{i=1}^n \{ E_{p(\theta | x^n)} [(log p(x_i | \theta))^2 ] - E_{p(\theta | x^n)} [log p(x_i|\theta) ]^2 \} }$

WAICでは現実値の計算に真の分布 $q(x)$ を必要としない。

BIC

BICを考えるときに、以下を仮定する。

真の分布は想定される確率モデルの中に含まれる
サンプルはi.i.d
$q(x)$ は確率モデルについて必ずしも正則でなくても仮定

モデルからデータが得られる確からしさとして周辺尤度は次のように定義されます。

$\displaystyle{ p(x^n) = \int p(x^n|\theta)\phi(\theta) d \theta }$

この周辺尤度を用いて次のような(ベイズ)自由エネルギーが定義される。

$\displaystyle{ F_n = -log \int p(x^n) = -log \int p(x^n|\theta)\phi(\theta) d \theta }$

次の条件が満たされている場合、

真の分布が確率モデルに対して正則
事後分布が正規分布に近似できる
nが十分に大きい

自由エネルギーは積分のラプラス近似の手法を用いて次のように近似することができる。これがBICの定義となる。

$\displaystyle{ BIC = -log \sum_{i=1}^n log p(x_i|\hat \theta) + \frac{d}{2} log n }$

WBIC

WBICは正則でないモデルにおいても、自由エネルギーを近似することができる。

WBICは次のように定義できる。

$\displaystyle{ WBIC = \int n L_n(\theta) \left [ \frac{\prod_{n=1}^n p(x_i|\theta)^\beta \phi(\theta)}{\int \prod_{n=1}^n p(x_i|\theta)^\beta \phi(\theta) d \theta} \right ] }$

ここで $L_n(\theta)$ は経験対数損失である。

$\displaystyle{ L_n(\theta) = - \frac{1}{n} \sum_{i=1}^n log p(x_i|\theta) }$

WBICは逆温度が $\beta = 1/log (n)$ の時の事後分布における期待であると言える。

MCMCの結果から自由エネルギーを推定する方法としてブリッジサンプリングが存在する。

ブリッジサンプリング

周辺尤度はモデルが複雑になると解析的に計算することが難しくなります。

MCMCを使ったシミュレーションによる積分計算の方法が、ブリッジサンプリングです。

ブリッジサンプリングの前に周辺尤度を得る方法として、ナイーブモンテカルロ法と重点サンプリング法が存在する。

ナイーブモンテカルロ法では、MCMCで事前分布から大量の乱数パラメータを生成し、各サンプルの尤度関数の期待値をとることで周辺尤度を計算する。

$\displaystyle{ \hat \theta_i \sim \phi (\theta), \hat p_{NM}(x^n) = \frac{1}{R} \sum_{i=1}^R p(x^n|\hat \theta_i) }$

この方法では、事前分布と事後分布に乖離がある場合はシミュレーションの効率が悪くなる。

重点サンプリング法は提案分布から乱数を生成し、各サンプルの尤度を事前分布と提案分布の比で調整してから平均する方法である。

$\displaystyle{ \hat \theta_i \sim [f:id:saltcooky:20210411214529p:plain$

g (\theta), \hat p_{IS}(x^n) = \frac{1}{R} \sum_{i=1}^R p(x^n|\hat \theta_i)\frac{\phi (\hat \theta_i)}{g(\hat \theta_i)} }]

ナイーブモンテカルロ法より、効率よく計算できるが、提案分布に何を選択するのかで変わってくる。

この分布は（1）事後分布より裾が重く（2）事後分布と形状が類似しており（3）事後分布と同じ台を持ち（4）評価が容易な分布であることが求められるとされている。

そのほかにも、一般化調和平均サンプリング法が提案されている。

$\displaystyle{ \hat \theta_j^* \sim \phi (\theta|x^n)\\ \hat p_{GHM}(x^n) = \left( \frac{1}{R}\sum_{i=1}^R \frac{1}{p(x^n|\hat \theta^*_i) } \frac{g(\theta^*_j)}{\phi (\theta^*_j)}\right) ^{-1} }$

この方法でも調整のために重点分布の設定を行う必要がある。

そして、ブリッジサンプリングでは、重点サンプリングと一般化調和平均サンプリングの両方のアルゴリズムの利点を取り入れた方法となっている。

具体的には、提案分布 $ɡ(\theta)$ からの乱数 $\theta_i$ と，事後分布[tex:p(\theta|xⁿ)] からの乱数 $\theta_j^*$ の両者を利用する。

$\displaystyle{ \hat \theta_j \sim g (\theta)\\ \theta_j^* \sim \phi (\theta|x^n)\\ }$

この提案分布では、事後分布と類似しており重なりが大きい分布が求められる。

$\displaystyle{ \hat p_{BS}(x^n) = \frac{\frac{1}{R_2} \sum_{i=1}^{R_2} p(x^n|\hat \theta_i)p(\hat \theta_i)h(\hat \theta_i)}{\frac{1}{R_1} \sum_{j=1}^{R_1} h(\theta_j^*)g(\theta_j^*)} }$

ここで $h(\theta)$ はブリッジ関数である(詳細についてはよくわからず)

Rstanでの算出

混合ガウス分布において混合数を変えた時のWAICとWBICを推定する。

利用したサンプルデータ次のように生成した。

generate_bimodal_data <- function(N, m1, m2, sd1, sd2, p, seed = 42){
  set.seed(seed)
  Y <- c(rnorm((1-p)*N, m1, sd1), rnorm(p*N, m2, sd2))
  return(Y)
}

X <- generate_bimodal_data(500, 0,5, 1, 1, 0.3)

WAIC

WAICを算出するための対数尤度を計算しつつ混合ガウス分布を推定するモデルを次のようなものとした。

data {
  int<lower=1> K;
  int<lower=1> N;
  vector[N] X;
}

parameters {
  simplex[K] p[N];
  ordered[K] mu;
  vector<lower=0, upper=20>[K] sigma;
}

transformed parameters{
  real theta[N,K];
  
  for(n in 1:N)
    for(k in 1:K)
       theta[n, k] = log(p[n, k]) + normal_lpdf(X[n] | mu[k], sigma[k]);
}

model {
  sigma ~ cauchy(0,2.5);
  mu ~ normal(0,10);
  for(n in 1:N)
    target += log_sum_exp(theta[n]);
}

generated quantities {
  vector[N] log_likelihood;
  vector[K] tmp[N];
  //int index;
  // real X_pred;
  for(n in 1:N){
    for(k in 1:K){
      tmp[n, k] = log(p[n, k]) + normal_lpdf(X[n] | mu[k], sigma[k]);
    }
    log_likelihood[n] = log_sum_exp(tmp[n]);
  }
}

MCMC結果からWAICを算出する関数は次にように定義します。

WAIC <- function(log_likelihood) {
  training_error <- - mean(log(colMeans(exp(log_likelihood))))
  functional_variance_div_N <- mean(colMeans(log_likelihood^2) - colMeans(log_likelihood)^2)
  waic <- training_error + functional_variance_div_N
  return(waic)
}

また、loo packageを用いた方法でも WAICを推定してみます。

loo::waic(extract(fit_model_waic)$log_lik)$waic/(2*length(df))

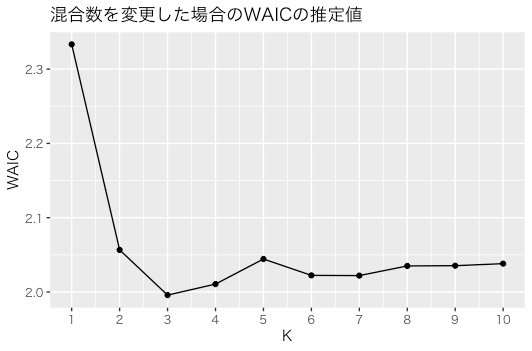
それぞれの結果は次にようになりました。

> res_mcmc_loop_waic
    k     waic waic.loo
1   1 2.336001 2.336002
2   2 2.061759 2.061882
3   3 2.002740 2.002835
4   4 2.009547 2.009646
5   5 2.021851 2.021954
6   6 2.016386 2.016470
7   7 2.015118 2.015195
8   8 2.018240 2.018328
9   9 2.018385 2.018463
10 10 2.016807 2.016873

対数から直接計算したものとloo::waicで算出したものはほぼ一緒になった。

対数から計算したWAICをグラフ化してみると次のようになった。

f:id:saltcooky:20210411214529p:plain

WBIC

WBICの計算はstanコードを変更することによる算出方法とbridgesampling packageを利用したブリッジサンプリングによる算出方法を試す。

対数情報からWBICを算出する関数は次にように定義します。

WBIC <- function(log_likelihood){
  -mean(rowSums(log_likelihood))
}

この関数を利用するためには、逆温度が1/log(データ数)の時の事後分布が必要になるため、上記のstanコードのmodelブロックを次のように変更する必要がある。

model {
  sigma ~ cauchy(0,2.5);
  mu ~ normal(0,10);
  for(n in 1:N)
    target += 1/log(N) * log_sum_exp(theta[n]);
}

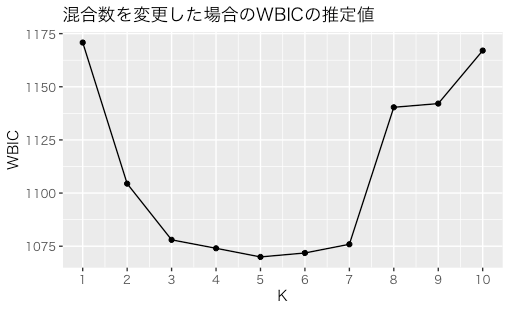
対数尤度から計算したWBICの変化をみてみました。

f:id:saltcooky:20210411194414p:plain

bridge samplingによるWBICの推定を行う関数を次のように定義した。

WBIC.bs <- function(model){
  bs <- bridge_sampler(model, method = "warp3")
  return(-logml(bs))
}

また、MCMCを実行する実行する時のiter数はかなり大きな値を設定しないと、bridge samplingを行う際にエラーとなってします。

今回はiter=10000, wurmup=1000とした。

実行時間がかなりかかるため、K=2,3の場合のみを計算し、事後対数からえたWBICと比較した。

	WBIC	WBIC(BS)
K=2	1104.143	1043.078
K=3	1445.512	1355.124

二つの方法で一致しませんでした。

他の簡単なサンプルで実行しましたが、やっぱり一致しませんでした。

名前はまだない

データ分析とかの備忘録か, 趣味の話か, はたまた

RstanでWAICとWBICの算出

はじめに

事前設定

AIC

WAIC

BIC

WBIC

ブリッジサンプリング

Rstanでの算出

WAIC

WBIC

参考