はじめに

ここ最近で機械学習と因果推論の融合が有名になってきました。

その中で、決定木(回帰木)のアルゴリズムを用いて条件付き処置効果(CATE)を推定するCausal Treeという手法の話がでてきています。

しかし、概要を聞いても何をしているのかよくわからないので、Causal Treeの提案者であるS.Atheyが書いた論文を読みました。

arxiv.org

Causal Treeでどのように条件付き処置効果(CATE)を推定しているのかまとめてみました。

といっても個人的なメモに過ぎません(免責事項)。いつも通り、少しずつ修正を加えていきます。

正直これらのスライドの方が簡潔でわかりやすいです。私も参考にさせていただきました。

計量経済学と機械学習の交差点入り口（公開用）

勉強会準備資料備忘：causal forest & r-learner - Speaker Deck

Causal Tree

基本的な考え方

木を作成した場合、同じ葉になったデータにおける共変量は近しいものになるはずです。この同じ共変量同士のデータを用いて推定された処置効果は、条件付き平均処置効果(CATE)であると言えます。

そのため、ここで作成される木は直接処置効果を推定することではなく(元々そんなことはできないのですが)、データをクラスタリングするような役割があります。

事前知識

因果推論

得られている値 $Y_i ^{obs}$ は、処置 $W_i$ によって異なる値が得られていると考えます。

$\begin{eqnarray} Y _i ^{obs} = Y_i (W_ i) = \left\{ \begin{array}{l} Y_i(0) & if W_i =0, \\ Y_i(1) & if W_i =1. \end{array} \right. \end{eqnarray}$

処置による効果は、次のように求めることができます。

$\tau_i = Y_i (1)-Y_i (0)$

また、処置群に割り当てられる確率は、傾向スコアと呼ばれています。

$e(x) = P(W_i = 1|X_i = x)$

傾向スコアで重み付けすることで強く無視できる割り当て条件が成り立ちます。

$W_i \perp (Y_i(1),Y_i(0)) | X_i$

この傾向スコアが等しいサンプル同士は背景情報が等しい=共変量の調整ができている言えます。

そして、傾向スコアを用いてマッチングや重み付け用いることで、平均処置効果(ATE)を推定することができます。

ここら辺の話は、こちらの書籍が参考になると思います。

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

作者:星野崇宏
発売日: 2009/07/29
メディア: 単行本

効果検証入門〜正しい比較のための因果推論/計量経済学の基礎

作者:安井翔太
発売日: 2020/01/18
メディア: 単行本（ソフトカバー）

一方で、共変量が異なれば処置の効果も異なってくると考えられます。この時のある共変量 $X_i$ における条件付き平均処置効果(CATE:conditional average treatment effect)は次にように定義できます。

$\tau (x) ≡ E[Yi(1) − Yi(0)|X_i = x$ ]

あるデータおける不偏推定量 $\hat \tau(x)$ を、求めることができるモデルを考えていきます。

回帰木(決定木)について

ここで特徴量空間 $X$ を分割した領域 or 木 $\Pi$ を考えます。

$\Pi = \{l_1, \dots , l_{\#(T)} \} , with \bigcup_{j=1} ^{\#(\Pi )} l_i=X$

ここで、 $l_i$ は $\Pi$ を構成する葉(leaf)、#( $\Pi$ ) は特徴量空間 $X$ を分割した数です。

枝の分岐は、分岐後の各葉に所属するデータにおけるMSE (Mean Squared Error) が小さくなるような、どの変数をどの値で区切るのかを探索していくこととなります。

この木における、 $x$ の条件付き平均値は、次にように表現できます。

$\displaystyle{ \mu (x ; \Pi ) \equiv E [ Yi | Xi \in l(x ; \Pi )] = E[\mu(X_i)|X_i \in l(x; \Pi)] }$

そして、ある葉の領域 $X_i$ のデータ(サンプル) $S$ で推定される期待値は、次にように表現できます。

$\displaystyle{ \hat \mu (x ;S, \Pi) \equiv \frac{1}{\#(i \in S : X_i \in l(x ; \Pi))} \sum_{\#(i \in S : X_i \in l(x ; \Pi))} Y_i }$

Causal treeための拡張したMSE基準

今回作成するCausal Treeは通常の回帰木と、二つの点が異なります。

一つ目は、何かしらの教師データがある結果を予測することではなくCATEを推定することです。

二つ目は、推定に用いるデータの使い方が異なります。

このような違いがあるため、木構造の推定を行うための最適化基準であるMSEは用いることができません。

論文では、Causal Treeの木構造を推定するための拡張した最適化基準を導入することが主題となっています。

通常の回帰木を作成する場合は、木構造の推定と各葉における統計量(期待値)の推定に同じデータを用います。論文では、この時の最適化基準をadaptive型の基準(と推定)と呼んでいました。

今回のCausal Treeでは、木構造の推定と各葉における効果の推定で異なるデータを用います。この時の最適化基準をHonest型の基準(と推定)と呼んでいました。

はじめに、因果効果ではなく一般的な条件付き期待値を推定するための最適化基準を導入します。 (のちに因果効果の推定に関する基準を導入します。)

最適化における基準

得られているデータを学習データ $S ^{tr}$ 、推定データ $S ^{est}$ 、テストデータ $S ^{te}$ の３つにランダムに分けておきます。

通常の回帰木では、MSEを用いて枝の分岐を行い木の構造を求めます。

Causal Treeでは、木構造の推定に用いる修正されたMSEを次のように定義しています。 $S ^{est}$ で作成した木 $\Pi$ で得られています。

$\displaystyle{ MSE(S ^{te},S ^{est},\Pi) \equiv \frac{1}{\#(S^{te})} \sum_{i \in S^{te}} \{ (Y_i - \hat \mu (X_i;S^{est,\Pi}))^2 - Y_i ^2\} }$

ここで、 $\Pi$ は $S ^{tr}$ で作成した木です。

この基準は、作成した木に対し推定データ $S ^{est}$ を入力して得られた推定値 $\hat \mu$ と実測値の誤差であると言えます。

そして、 $(S^{te},S^{est})$ にわたあって予測される(expected)MSEは次にようになります。

$\displaystyle{ EMSE(\Pi) \equiv E_{S ^{te},S ^{est}} [MSE(S ^{te},S ^{est}, \Pi) ] \tag{1} }$

木構造の推定を行うために最大化する目的関数 $Q ^H$ は、次のように定義します。

$\displaystyle{ Q ^H (\pi) \equiv -E_{S^{tr},S^{te},S^{est}} [MSE(S ^{te},S ^{est}, \pi (S^{tr})) ] }$

これはHonest型の推定のための目的関数です。

adaptive型の推定のための目的関数 $Q ^C$ は、次のように定義します。

$\displaystyle{ Q ^C (\pi) \equiv -E_{S^{tr},S^{te}} [MSE(S ^{te},S ^{tr}, \pi (S^{tr})) ] }$

それぞれのメリットデメリットは、Honest型の場合は過学習が防げるが学習データのサンプル数が少なくなること、adaptive型は学習データ数は確保できるが過学習状態に陥ることがあります。

枝の分岐基準

Honest型の推定アルゴリズムでは、2つの方法でCARTを変更します。

上で定義したEMSEを次にように変形して拡張します。

$\displaystyle{\begin{eqnarray} −EMSE(Π) = -E_{(Y_i,X_i),S ^{est}}[ (Y_i - \hat \mu (X_i;S ^{est},\Pi))^2 - Y_i ^2 ] \\ -E_{X_i,S ^{est}}[ (\hat \mu(X_i;S ^{est},\Pi)-\mu(X_i;\Pi))^2 ] \\ = E_{X_i}[ \mu^2 (X_i;\Pi) ]-E_{X_i,S ^{est}}[ V(\hat \mu ^2 (X_i;S ^{est},\Pi)) ] \tag{2} \end{eqnarray} }$

右辺の第二項は、各葉において推定された期待値の分散の不偏推定量です。

$\displaystyle{ \hat V(\hat \mu ^2 (X_i;S ^{est},\Pi)) \equiv \frac{S_{S ^{tr}(l(x ; \Pi ))} ^2}{N ^{est}(l(x ; \Pi ))} }$

ここで、 $S_{S ^{tr}(l)} ^2$ は葉 $l$ に該当する学習データから求められる分散、 $N ^*$ はデータ $S ^*$ におけるサンプル数です。

各葉の領域に該当するサンプルの割合が学習データと推定データでほぼ同じであると仮定すると、この分散推定量は次のように近似できます。

$\displaystyle{ \begin{eqnarray} E_{X_i,S ^{est}}[ V(\hat \mu ^2 (X_i;S ^{est},\Pi)) ] \equiv \frac{1}{N ^{est}} \sum_{(l \in \Pi)} S_{S ^{tr}} ^2(l) \end{eqnarray} }$

右辺の第一項の $\mu ^2$ の期待値は、学習データを用いて推定された平均値と分散を用いることで次のように求めることができます。

$\displaystyle{ \begin{eqnarray} \hat E [\mu ^2(x;\Pi) ]=\hat \mu ^2 (X_i;S ^{tr},\Pi) - \frac{S_{S ^{tr}(l(x ; \Pi ))} ^2}{N ^{tr}(l(x ; \Pi ))} \end{eqnarray} }$

これらを組み合わせるとEMSEの不偏推定量を得ることができます。

$\displaystyle{ \begin{eqnarray} \widehat{EMSE}(S_{tr}, \Pi) \equiv \frac{1}{N ^{tr}} \sum_{i \in S ^{tr}} \hat \mu ^2 (X_i;S ^{tr},\Pi)-\left( \frac{1}{N ^{tr}}+\frac{1}{N ^{est}}\right) \sum_{(l \in \Pi)} S_{S ^{tr}} ^2(l) \\ \end{eqnarray} }$

そして、データの分割時に $N ^{tr}=N ^{est}$ とすることができるので、最終的な拡張された基準は次にようになります。

$\displaystyle{ \begin{eqnarray} \widehat{EMSE}(S_{tr}, \Pi) \equiv \frac{1}{N ^{tr}} \sum_{i \in S ^{tr}} \hat \mu ^2 (X_i;S ^{tr},\Pi)-\frac{2}{N ^{tr}} \sum_{(l \in \Pi)} S_{S ^{tr}} ^2(l) \tag{3} \end{eqnarray} }$

通常のCART アルゴリズムで用いられるMSEと異なり、分散に関する二項目が加えられています。

この $-EMSE$ の最大化は、各葉における平均値は最大化しつつ、分散はなるべく小さくすることを目指すことを意味します。

また、学習データのみで木構造を推定することができることも重要な特徴となります。

条件付き処置効果の推定

ここからは、これまで定義してきたMSEとEMSEを拡張し、次の条件付き処置効果 $\tau$ を推定できるようにしていきます。

$\displaystyle{ \begin{eqnarray} \tau \equiv E[Y_i(1)-Y_i(0)| X_i \in l( x; \Pi) ] \end{eqnarray} }$

ここで、各群における目的変数の平均値は次のように定義できます。

$\displaystyle{ \begin{eqnarray} \hat \mu (\omega,x;S,\Pi) \equiv \frac{1}{\#({i\in S_{\omega};X_i \in l(x;\Pi)})} \sum_{i \in S_{\omega};X_i \in l(x;\Pi)} Y_i ^{obs} \end{eqnarray} }$

Causal Treeで求めるべき条件付き因果効果は次のように定義できます。

$\displaystyle{ \begin{eqnarray} \hat \tau (x;S,\Pi) \equiv \hat \mu (\omega =1,x;S,\Pi) - \hat \mu (\omega = 0,x;S,\Pi) \end{eqnarray} \tag{4} }$

式3で定義したMSEの $\hat \mu$ に $\hat \tau$ を当てはめると次にようになります。

$\displaystyle{ \begin{eqnarray} MSE_{\tau}(S ^{te},S ^{est},\Pi) \equiv \frac{1}{\#(S^{te})} \sum_{i \in S^{te}} \{ (\tau_i - \hat \tau (X_i;S^{est,\Pi}))^2 - \tau_i ^2\} \tag{5} \end{eqnarray} }$

そして、EMSEも次のようになります。

$\displaystyle{ \begin{eqnarray} EMSE_{\tau}(\Pi) \equiv E_{S^{te},S^{est}} [MSE_{\tau}(S ^{te},S ^{est},\Pi) ] \end{eqnarray} }$

しかし、 $\tau$ は観測不可能であるため、これらの基準も算出が不可能です。

ここで、式2のEMSEに $\hat \mu$ に $\hat \tau$ を当てはめてみます。

$\displaystyle{ \begin{eqnarray} - \widehat{EMSE}_{\tau}(\Pi) = E_{X_i}[ \tau^2 (X_i;\Pi) ]-E_{X_i,S ^{est}}[ V(\hat \tau ^2 (X_i;S ^{est},\Pi)) ] \end{eqnarray} }$

式3の形に変形することができるそうで、実際には次のような式となります。

この式をみると観測可能なデータのみでEMSEの推定量を定義することができています。

$\displaystyle{ \begin{eqnarray} \widehat {EMSE}_{\tau}(S_{tr}, \Pi) \equiv \frac{1}{N ^{tr}} \sum_{i \in S ^{tr}} \hat \tau ^2 (X_i;S ^{tr},\Pi)- \frac{2}{N ^{tr}} \sum_{(l \in \Pi)} \left ( \frac{S_{S ^{tr}_{treat}} ^2(l)}{p} + \frac{S_{S ^{tr}_{control}} ^2(l)}{1-p} \right) \\ \end{eqnarray} \tag{6} }$

この $-EMSE$ の最大化は、各葉における因果効果(処置群と対称群の差)を最大化しつつ、分散はなるべく小さくすることを意味しています。

実際のHonestの場合のCausal Treeの生成では、枝の分割と枝刈りを $− \widehat{EMSE} (S ^{tr}, \Pi)$ 行います。式4に従い、 $S ^{est}$ を用いて各葉におけるCATEの推定します。そして、 $S ^{te}$ に対してCATEの予測することができるようになります。

adaptiveな場合のCausal Treeの生成もでき、枝の分割と枝刈りを $− \widehat{MSE} (S ^{tr} , S ^{tr} , \Pi)$ を用います。

Causal Forest

Causal Treeは通常の回帰木と動作は変わりないため、複数のTreeのアンサンブルを行うことができます。

それがCausal TreeをRandam Forestの構造に拡張したものがCausal Forestです。

arxiv.org

詳しい話は、また機会があればまとめたいと思います。

(Causal treeの文章を作成するので力尽きてしまいました)

ここら辺を参考にしていただけらばと思います。

RでCausal Treeを使ってみる

RのCausal TreeのパッケージcausalTreeはSusan AtheyのGitHubリポジトリにあります。

インストールをしてみます。

devtools::install_github("susanathey/causalTree")

用いたのはRight heart catheterization datasetという心臓カテーテルに関するデータです。

> dataSet = read.csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/rhc.csv")
>
> table(dataSet[,c("swang1", "death")])
                death
swang1     No  Yes
  No RHC 1315 2236
  RHC        698 1486

集計に基づく処置効果は5%程度のようです。

> 1486/(698+1486) - 2236/(1315+2236)
[1] 0.05072115

CT_df <- dataSet %>% 
  dplyr::select(death , swang1, age , sex , race , edu , income , ninsclas , cat1 , das2d3pc , dnr1 , ca , surv2md1 , aps1 , scoma1 , wtkilo1 , temp1 , meanbp1 , resp1 , hrt1 , pafi1 , paco21 , ph1 , wblc1 , hema1 , sod1 , pot1 , crea1 , bili1 , alb1 , resp , card , neuro , gastr , renal , meta , hema , seps , trauma , ortho , cardiohx , chfhx , dementhx , psychhx , chrpulhx , renalhx , liverhx , gibledhx , malighx , immunhx , transhx , amihx) %>% 
  mutate(death = if_else(death=="Yes",1,0),
         swang1 = if_else(swang1=="No RHC",0,1))

傾向スコアマッチングで平均処置効果を算出したいと思います。

PS_model = glm(swang1 ~ .,
               family = binomial(link = "logit"), 
               data = CT_df %>% dplyr::select(-death))

PSMatching <- Match(Y = as.integer(CT_df$death)-1, 
                    Tr = (CT_df$swang1==1),
                    X = PS_model$fitted.values,
                    M = 1,
                    caliper = 0.1,
                    ties = FALSE,
                    replace = FALSE)
summary(PSMatching)

結果は次にようになりました。

Estimate...  0.063472 
SE.........  0.016459 
T-stat.....  3.8564 
p.val......  0.00011506 

Original number of observations..............  5735 
Original number of treated obs...............  2184 
Matched number of observations...............  1544 
Matched number of observations  (unweighted).  1544 

Caliper (SDs)........................................   0.1 
Number of obs dropped by 'exact' or 'caliper'  640

平均処置効果は6.3%と単純な集計で得られる値よりも大きくなっています。

それでは、Causal treeを作成しいきます。

データの6割を学習データ、4割を予測対象のデータとしました。

CT_df.tr <- CT_df %>% sample_frac(0.6)
CT_df.te <- anti_join(CT_df,CT_df.tr)

causaltree関数において、splitとCVにHonest型の最適化を行うのかadaptive型の最適化を行うのか設定できます。それぞれ、split.Honest、cv.Honest引数で設定します。

causal_tree <- causalTree(death ~ .,
                          data = CT_df.tr %>% dplyr::select(-swang1), 
                          treatment = CT_df.tr$swang1,
                          split.Rule = "CT", 
                          cv.option = "CT", 
                          split.Honest = T, 
                          cv.Honest = T, 
                          split.Bucket = F, 
                          xval = 5, 
                          cp = 0, 
                          minsize = 30)

opcp <- causal_tree$cptable[,1][which.min(causal_tree$cptable[,4])]

causal_tree_pruned <- prune(causal_tree, opcp)

得られた木構造を見てみます。

rpart.plot(causal_tree_pruned, roundint=FALSE)

わかりにくいですが、一部のデータではCATEが30%となるようです。

f:id:saltcooky:20200112235030p:plain

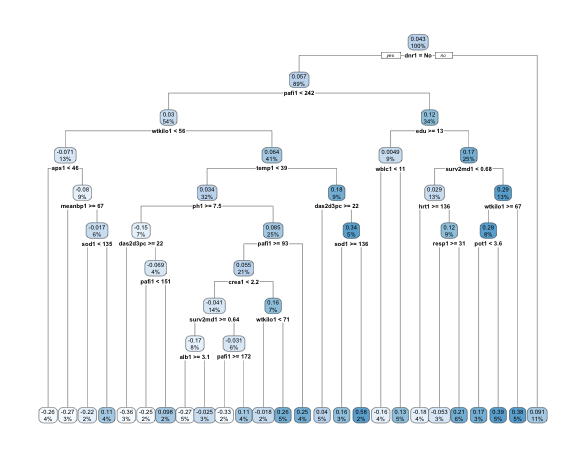
得られたCausal Treeを用いてテストデータにおけるCATEを予測させてます。

est_treat <- predict(causal_tree_pruned, CT_df.te)

予測値のヒストグラムは次にようになりました。

hist(est_treat)

f:id:saltcooky:20200112235010p:plain

平均処置効果をみてみると概ね傾向スコアマッチングの時と同じような値となりました。

> mean(est_treat)
[1] 0.06004903

もちろん、変数重要度も算出することができます。

f:id:saltcooky:20200117001703p:plain

なお、causalForest関数を用いることで、causalForestも利用できるそうです。

名前はまだない

データ分析とかの備忘録か, 趣味の話か, はたまた

Causal Treeはどうやって個別の因果効果を推定しているのかを整理(しきれなかった)