はじめに
最近、教師データを作成する際に質の高いデータが欲しいなとという思いが強くなってきました。
そんなときにクラウドソーシングにおけるラベルの品質管理という話を知りました。
少し調べてみましたので、まとめて用いられている手法を実装してみます。
クラウドソーシングの品質管理
クラウドソーシングにおいて、一人のワーカが行ったラベリングでは、機械学習の教師ラベルとして用いるには質が劣ってしまいます。
タスクの難易度により生まれる解答の個人差や金銭のみを目的としたワーカが、でたらめな回答をしてしまうことがあるためです。
この状態を解消するために、複数のワーカにラベリングを行ってもらい結果を統合します。
しかし、単純な多数決では上記のような質の悪いワーカの回答にひっぱられてしまい、得られたラベルの質も悪くなってしまいます。
そこで、複数のワーカのラベリングから真のラベルを推定してラベルの品質を高く保つ手法があります。
検索すると次のような論文が出てきました。
https://hkashima.github.io/publication/JSAI_crowds.pdf
こちらでは、クラウドソーシングにおける真値に近いラベル推定についての概要が紹介されていました。
同じ著者らが書いた書籍としてはこちらがありました。
こちらでは、ヒューマンコンピュテーションといくつかのラベル推定モデルが紹介されていました。
また、KDD2019でYandexがクラウドソーシングについてのハンズオンセッションを行っており、その時の資料も参考になりました。
https://research.yandex.com/tutorials/crowd/kdd-2019
それぞれのラベル推定モデルは、EMアルゴリズムによりパラメータ推定を行っています。
個人的にはstan力を付けたいので、ベイズ推定を行う場合についてを検索しました。
次のような解説論文が出てきました。
https://www.mitpressjournals.org/doi/pdf/10.1162/tacl_a_00040
今回はこれらを参考に簡単に紹介し、rstanにより実装を行いました。
潜在ラベルモデル
真のラベル推定には、潜在ラベルモデルと呼ばれるモデルを用います。
潜在ラベルモデルは、真のラベルは潜在変数であると仮定したモデルです。
また、得られたラベルはワーカの能力やタスク難易度により影響を受けていると考えたものです。
グラフィカルモデルで示すと次にようになります。

が真のラベルです。
は各評価タスク/評価対象
の異質性です。
は各ワーカ
の異質性や固有能力です。
が各ワーカ
が対象
を評価したラベルです。
潜在ラベルモデルにはいくつかの種類が存在しており、タスクの難易度やワーカの能力差を加味したもの、レビューのスコアリングのような順序統計量としたものなどです。
- Dawid and Skene model
- Generative model of Labels, Abilities, and Difficulties
- MiniMax Conditional Entropy model
実際のクラウドソーシングでは、これらのモデルによりワーカの能力等を推定することで質の悪いワーカの抽出やワーカの能力にあった報酬設計、タスクの難易度の設計等を行っているようです。
今回は二つのモデルを紹介しようと思います。
Dawid and Skene model
潜在ラベルモデルの中でも、ワーカの評価は各タスクでばらつくと仮定したモデルです。
タスクごとの難易度の違いは加味していません。
グラフィカルモデルで示すと次にようになります。
は潜在パラメータです。
はワーカの評価パターンの行列です。
これらに基づいて、評価値が得られているとするモデルです。
RStanで実装
Rstanコードは次のような感じです。 解説論文に付属していたコードをほどんどそのまま持ってきています。
data {
int<lower=1> W;
int<lower=2> K;
int<lower=1> N;
int<lower=1> I;
int<lower=1, upper=I> ii[N];
int<lower=1, upper=W> jj[N];
int<lower=1, upper=K> y[N];
}
transformed data {
vector[K] alpha = rep_vector(1,K);
vector[K] eta = rep_vector(1,K);
}
parameters {
simplex[K] pi;
simplex[K] beta[W, K];
}
transformed parameters {
vector<upper=0>[K] log_q_c[I];
vector<upper=0>[K] log_pi;
vector<upper=0>[K] log_beta[W, K];
log_pi = log(pi);
log_beta = log(beta);
for (i in 1:I)
log_q_c[i] = log_pi;
for (n in 1:N)
for (k in 1:K)
log_q_c[ii[n],k] = log_q_c[ii[n],k] + log_beta[jj[n],k,y[n]];
}
model {
for(w in 1:W)
for(k in 1:K)
beta[w,k] ~ dirichlet(eta);
pi ~ dirichlet(alpha);
for (i in 1:I)
target += log_sum_exp(log_q_c[i]);
}
generated quantities {
simplex[K] q_z[I];
for(i in 1:I)
q_z[i] = softmax(log_q_c[i]);
}
適用したデータは、潜在クラス分析を行うためのパッケージpoLCAに含まれている7人の病理学者が118件の子宮頸ガンかどうかを二値評価したデータです。
モデルをキックするコードは次のような感じです。
実行時間はMacBook Pro (15-inch, 2018)で、1分弱ぐらいでした。
library(tidyverse) library(rstan) library(poLCA) # 計算の並列化 rstan_options(auto_write = TRUE) options(mc.cores = parallel::detectCores()) # データの整形 ano_data <- carcinoma %>% sample_n(20) ano_stan_data <- unlist(ano_data) W <- ncol(ano_data) K <- 2 N <- length(ano_stan_data) I <- nrow(ano_data) ii <- rep((1:I), W) jj <- rep(1:W, each=I) run_data <- list(W = W, K = K, N = N, I = I, ii = ii, jj = jj, y = ano_stan_data) # DSモデル推定 ds_resalts <- stan(file = "DS.stan", data = run_data, seed = 42, iter = 4000, warmup = 2000, chains = 4, control = list(adapt_delta = 0.98, max_treedepth = 15))
推定の収束を判断してみます。
library(bayesplot) mcmc_rhat(rhat(ds_resalts))

収束してそうですね。
サンプリングに自己相関性がないことも確認しました。
それぞれのワーカの回答パターンを見てみたいと思います。
beta[a,b,c]はa番目のワーカが、正解がbのタスクにcと答える確率の事後分布です。 また、bとcが一致しているということは正しい正解を選択できる確率でもあります。
2のワーカは1を1(ガンでないをガンでない)、3,4,6のワーカは2を2(ガンをガン)と診断できないことが多いようです。

Generative model of Labels, Abilities, and Difficulties
このモデルでは、ワーカの能力差とタスクの異質性を加味したモデルです。
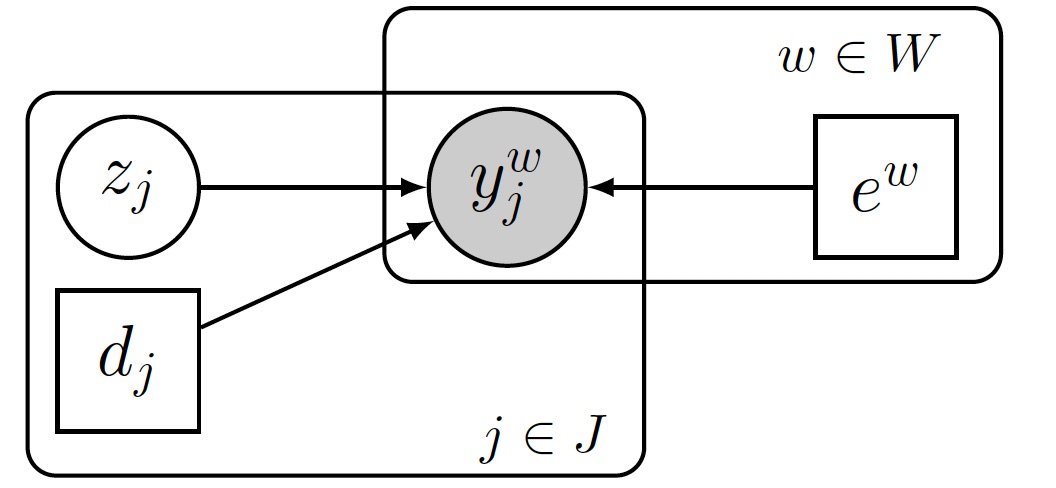
グラフィカルモデルで示すと次にようになります。
は、タスクの難易度を意味する潜在パラメータです。
は、ワーカの能力や個人差を意味する潜在パラメータです。
ワーカの能力とタスクの難易度と正解確率の関係は次のようになっています。
は項目反応理論の評価モデルです。
RStanで実装
Rstanコードは次のような感じです。
本来なら、 theta[W]に対して<lower=0>の制約は設けません。しかし、設けない場合に符号について不定性が生まれてしまい、あるチェインは正に、別のチェインは負に推定されて、事後分布が双峰になってしまいます。
コードの問題点やもっとこうした方がいいとかありましたら、指摘してもらいたいです。
data {
int<lower=1> W;
int<lower=2> K;
int<lower=1> N;
int<lower=1> I;
int<lower=1, upper=I> ii[N];
int<lower=1, upper=W> jj[N];
int<lower=1, upper=K> y[N];
}
transformed data {
simplex[K] z[I];
for (i in 1:I){
for (k in 1:K){
z[i, k] = 1.0/K;
}}
}
parameters {
real<lower=0> theta[W];
real<lower=0> d[I];
}
transformed parameters {
vector<lower=0, upper=1>[K] pr[W, I];
vector<upper=0>[K] log_q_c[I];
matrix<lower=0, upper=1>[W, I] a;
for (w in 1:W){
for (i in 1:I){
a[w, i] = 1/(1+exp(-1*theta[w]*d[i]));
for (k in 1:K)
if(y[I*(w-1)+i]==k){
pr[w,i,k] = a[w,i];
}else{
pr[w,i,k] = (1-a[w,i])/(K-1);
}
}
}
for (i in 1:I)
log_q_c[i] = log(z[i]);
for (n in 1:N) {
for (k in 1:K) {
log_q_c[ii[n],k] = log_q_c[ii[n],k] + log(pr[jj[n],ii[n],k]);
}
}
}
model {
for(w in 1:W){
theta[w] ~ normal(0, 4);
}
for(i in 1:I){
d[i] ~ lognormal(0,sqrt(0.5));
target += log_sum_exp(log_q_c[i]);
}
}
generated quantities {
simplex[K] q_z[I];
for(i in 1:I)
q_z[i] = softmax(log_q_c[i]);
}
モデルをキックするコードは次のような感じです。
# GLAD法 glad_resalts <- stan(file = "GALD.stan", data = run_data, seed = 42, iter = 4000, warmup = 2000, chains = 4, control = list(adapt_delta = 0.98, max_treedepth = 15))
実行時間は、10分弱だったと思います。
サンプリングが収束しているかを確認します。
mcmc_rhat(rhat(glad_resalts))
概ね収束していると判断して良さそうです。
サンプリングの自己相関性がないことも確認しました。

こちらのリポジトリにあるpythonでGLAD法を実装したものと結果を比較しました。
推定されたワーカの能力値の違いを確認してみました。

次に推定された診断対象の違い確認してみました。

スケールが異なるものの、両者の相関が高い状態にあるため推定はできているようです。
また、ほぼ推定されたラベルは一致しています。 2件でラベルが異なっていますが、2である確率が0.5付近であり判断が揺らぐものであるようです。
> table(python_label$z, stan_labels$z) 1 2 1 65 0 2 2 51
推定された各ワーカの能力を確認してみます。
samples <- as.array(glad_resalts) # ワーカーの能力の分布 mcmc_areas(samples, regex_pars = "^theta\\[", prob = 0.95, prob_outer = 1, point_est = "mean")

Gの判別は最も2(=ガンである)と判断しやすく、DとFは1(=ガンでない)と判断してしまうことが多いようです。(実際にデータを確認すると解答傾向が他の人と異なります)
終わりに
今回は2つのモデルについてstanで実装しました。
特にGLAD法はワーカの能力が推定できる点が、非常に良いですね。 能力の分析結果をワーカへフィードバックすることで、より良いラベリングにつなげるようなサイクルに応用できそうですね。
今後は、レーティングのような順序のある評価値における真のラベル推定を行うモデルを実装してみたいと思います。
参考
- “Maximum Likelihood Estimation of Observer Error-Rates Using the EM Algorithm”, 1979
Whose vote should count more: Optimal integration of labels from labelers of unknown expertise,2009
python GALD GitHub - notani/python-glad: A Python Implementation of GLAD