はじめに
数年前のセミナーか学会でTMLEの概要の説明を聞いたことがあります。
しかし、詳細については理解していないため、今回簡単にまとめたいと思います。
概要
このページが非常に丁寧に方法論と手順を説明していました。
特にこちらのチートシートが非常にわかりやすいです。

簡単にTMLEをまとめると
Targeted Maximum Likelihood Estimation (TMLE:ターゲット最尤推定)は、関心のある統計量を推定するためのセミパラメトリック推定フレームワーク
TMLEを使用すると、データの分布に最小限の仮定を置く機械学習モデルを使用できる
最終的なTMLE推定値は、通常のMLの推定値とは異なり統計的推論の有効な標準誤差の算出が行うことができる
TMLEの考え方
TMLEと関連する因果効果推定のフレームワークにsuper learnerがあります。
super learnerは以下のような特徴があげられる。
この特性をアップデートするのがTMLEである。
具体的には機械学習における柔軟なモデルを用いながら、ターゲットの推定値に対してバイアスと分散の既知の漸近特性を持たせることを主眼としている。
機械学習を用いて推定した結果変量を入力とするモデルを考え、そのパラメータを最尤推定により推定するセミパラメトリック推定法が用いられる.
セミパラメトリック推定方法では、従来のパラメトリックモデル(線形回帰やロジスティック回帰など)を使用して取得するよりもターゲット量に近い最終的な推定値を取得できるとされている。
また、Doubly Robust推定の考え方に近く、アウトカムモデルまたは傾向スコアモデルのどちらかを適切に推定することができれば、処置効果の推定が行えるとされている。
TMLEの手順
目的変数を推定するモデルの作成
全ての処置変数と共変量
を用いて目的変数
を推定するモデルを作成する。
このモデルには、仮定の少ない柔軟なモデルを用いるために機械学習やそれらのアンサンブルモデルを用いても良い。
目的変数の推定
上記で推定したモデルを用いて、全体を処置群に割り当てた場合と、全体を対照群に割り当てた場合の結果を推定することができる。
各観測値ごとに結果を推定しておく。
傾向スコアの計算
共変量を用いて傾向スコアを計算。
このモデルにはロジスティックモデルを用いる。
推定されたモデルを用いて、処置の逆確率と、非処置の負の逆確率を推定する。
これらを用いてclever covariateと呼ばれる情報を生成する
推定のアップデート
ATEの推定値が漸近的に偏らないように、以下のモデルを仮定し、初期結果の推定値をclever covariateaで更新します。
ここでは変動パラメータと呼ばれ、最尤推定により推定することで推定量
を修正する。
CATEとATEの推定
CATEは各サンプルにおける処置ありと治療なしの差分から計算。
ATEは処置ありと治療なしの更新された結果推定値の平均差から計算。
RでTMLEを実行する
RでTMLEを実行するにはtmle packageを用いる。
今回はサンプルコードをベースに挙動を確認する。
はじめに学習用データを生成します。 モデルを複雑な形にするためにアウトカムモデルを非線形な形にしています。
n <- 250 W <- matrix(rnorm(n*3), ncol=3) A <- rbinom(n,1, 1/(1+exp(-(.2*W[,1] - .1*W[,2] + .4*W[,3])))) Y <- 1.2*A + 2*W[,1] + W[,3] + W[,2]^2 + W[,1] * W[,3] + 0.3 * W[,3]^2+ rnorm(n) tmle_df = data.frame(Y, A, W)
真の処置効果を1.2と設定したが、単純な集計では2倍近く処置効果があると推定してしまっている。
> tmle_df %>% + group_by(A) %>% + summarise(honest_effect = mean(Y)) # A tibble: 2 × 2 A honest_effect <int> <dbl> 1 0 0.802 2 1 2.97
比較のために単純な回帰モデルでも確認しておく。
simple_model <- lm(Y ~ ., data =tmle_df)
結果は以下の通り
> summary(simple_model) Call: lm(formula = Y ~ ., data = tmle_df) Residuals: Min 1Q Median 3Q Max -3.9748 -1.4941 -0.2996 1.0213 10.7271 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 1.279644 0.205906 6.215 2.20e-09 *** A 1.338102 0.284593 4.702 4.31e-06 *** X1 1.967265 0.145563 13.515 < 2e-16 *** X2 -0.008661 0.130301 -0.066 0.947 X3 0.906289 0.135040 6.711 1.33e-10 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.179 on 245 degrees of freedom Multiple R-squared: 0.5258, Adjusted R-squared: 0.5181 F-statistic: 67.92 on 4 and 245 DF, p-value: < 2.2e-16
TMLEを実行する。
この時の引数は以下のようになっている。
- Y:目的変数
- A:処置変数
- W:共変量
- Z:中間変数
res_tmle <- tmle(Y,A,W)
そのほかにも次のような引数がある。
- Delta:欠損を表現する表現する値
- family:glmと同様に目的変数の分布を指定することができる
- Qform:アウトカムモデルの定義
- gform:介入モデルの定義
- V:CV数
結果を見ると、推定されたATEとATTとATUを確認することができる。
単純な回帰モデルより分散が小さくなっていることは確認できる。
> res_tmle Additive Effect Parameter Estimate: 1.0475 Estimated Variance: 0.034315 p-value: 1.5629e-08 95% Conf Interval: (0.68438, 1.4105) Additive Effect among the Treated Parameter Estimate: 1.0821 Estimated Variance: 0.037115 p-value: 1.9427e-08 95% Conf Interval: (0.70454, 1.4597) Additive Effect among the Controls Parameter Estimate: 0.99743 Estimated Variance: 0.037458 p-value: 2.5558e-07 95% Conf Interval: (0.61809, 1.3768)
summaryにかけると、より詳細な結果を確認できる。
アウトカムモデルと処置モデルには、SuperLearnerとしてglmとBARTとLasso系モデルのアンサンブルを用いているようです。
上記の引数をうまく設定すると制御できるようだが、細かい部分までは調べられていない。
> summary(res_tmle) Initial estimation of Q Procedure: cv-SuperLearner, ensemble Model: Y ~ SL.glm_All + tmle.SL.dbarts2_All + SL.glmnet_All Coefficients: SL.glm_All 0 tmle.SL.dbarts2_All 0.9947809 SL.glmnet_All 0.005219127 Cross-validated R squared : 0.7969 Estimation of g (treatment mechanism) Procedure: SuperLearner, ensemble Empirical AUC = 0.6507 Model: A ~ SL.glm_All + tmle.SL.dbarts.k.5_All + SL.gam_All Coefficients: SL.glm_All 0 tmle.SL.dbarts.k.5_All 0 SL.gam_All 1 Estimation of g.Z (intermediate variable assignment mechanism) Procedure: No intermediate variable Estimation of g.Delta (missingness mechanism) Procedure: No missingness, ensemble Bounds on g: (0.0573, 1) Bounds on g for ATT/ATE: (0.0573, 0.9427) Additive Effect Parameter Estimate: 1.0475 Estimated Variance: 0.034315 p-value: 1.5629e-08 95% Conf Interval: (0.68438, 1.4105) Additive Effect among the Treated Parameter Estimate: 1.0821 Estimated Variance: 0.037115 p-value: 1.9427e-08 95% Conf Interval: (0.70454, 1.4597) Additive Effect among the Controls Parameter Estimate: 0.99743 Estimated Variance: 0.037458 p-value: 2.5558e-07 95% Conf Interval: (0.61809, 1.3768)
終わりに
いつTLMEを用いるべきかが気になります。
ざっと考えたところ、以下のような場合になると考えられる。
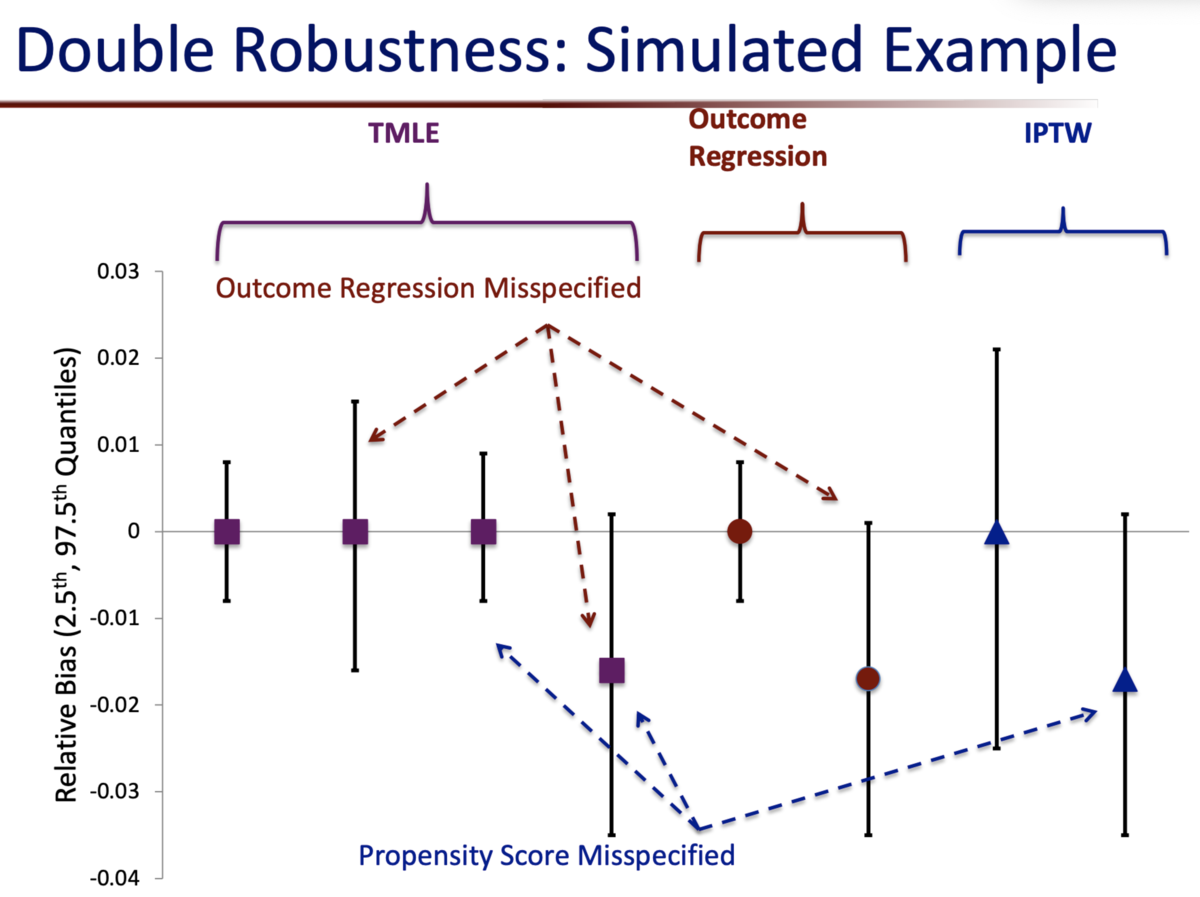
ちなみにこちらの資料では、回帰モデルとIPW推定の場合を比較しているが、回帰モデルでも適切に設定できれば、TMLEと同程度の精度で推定することができらしい...
細かい部分はこれから調べていきたい。