はじめに
Metaが開発しているMMMパッケージの存在を知りました。
facebookexperimental.github.io
非常に良さそうなので、どのようなパッケージなのかを調べまとめました。
MMMについてはこちらに簡単にまとめています。
概要
Meta(facebook)が作成したマーケティングミックスモデリング(MMM)を手軽に行うためのパッケージです。
Robynは、Marketing Scienceの実験的な、半自動化されたオープンソースのマーケティングミックスモデリング(MMM)パッケージと定義しています。
さまざまな機械学習手法(リッジ回帰、ハイパーパラメーター最適化のための多目的進化的アルゴリズム、トレンドとシーズンのための時系列分解、予算配分のための勾配ベースの最適化など)を使用して、モデルの推定を行う。
作成した理由として、以下のような要素が掲げられています。
Metaは、MMMの取り組みと3つの方法を以下のように表現しています。
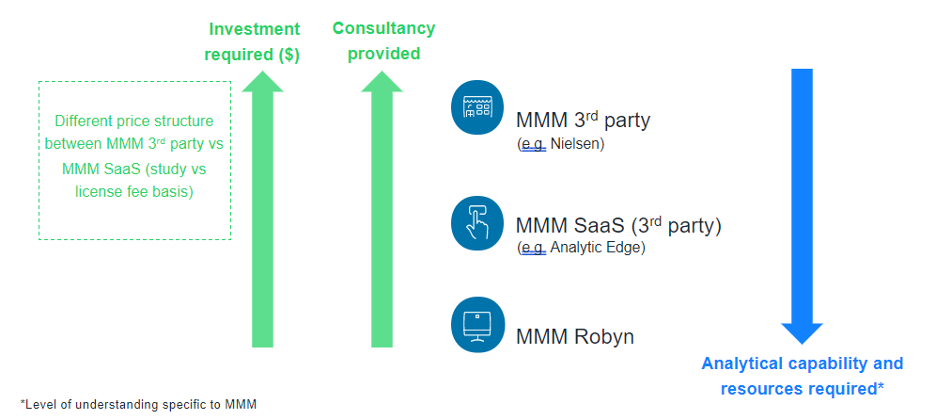
そして、3つの方法のメリットとデメリットを比較している。
①サードパーティのMMMベンダーとの連携
長所:最小限の時間と労力で済み、MMMの結果をベンチマークと比較できる
短所:高額な費用が発生する
②半自動化されたMMMツールまたはサービスとしてのソフトウェア(Saas)プラットフォームの使用
長所:専門性の低いMMMまたは分析の専門知識を持っている人に適しており、MMMベンダーと協力するよりも安価
短所:MMMベンダーと協力するよりも相談しにくい
③Robynを用いて社内でMMMソリューションを構築する
長所:MMMを実行するための継続的なコスト(人員と時間)がかからない
短所:社内で分析/データサイエンスを機能させる必要であり、3つの中で最も内部の時間とリソースへの投資が必要
内部的に時系列のモデリングを行っているのはこちらもMetaが開発したprophetです。
このようなパッケージを作成してきたMetaだから可能にしたパッケージかもしれません。
Robynを試す
インストール
Robynを実行するにはRのバージョンが4.0.0以上が求められる。
また、PythonライブラリNevergradも必要となるためreticurate packageを用いて利用できるようにする。
install.packages("reticulate") library(reticulate)
nevergrad イブラリをインストールするには、2つのオプションがある。
# オプション1:PIPを使用する virtualenv_create("r-reticulate") py_install("nevergrad", pip = TRUE) use_virtualenv("r-reticulate", required = TRUE)
# オプション2:condaを使用する conda_create("r-reticulate") conda_install("r-reticulate", "nevergrad", pip = TRUE) use_condaenv("r-reticulate")
インストール後もnevergradをインポートできない場合は、Pythonファイルパスを探し、以下を実行。
use_python("~/Library/r-miniconda/envs/r-reticulate/bin/python")
私の場合はcondaを利用したました。
また、nevergradを利用する前に幾つかのライブラリのインストールを行いました。
conda_install("r-reticulate", c("cycler","fonttools","kiwisolver","pillow"), pip = TRUE) conda_install("r-reticulate", "statsmodels", pip = TRUE)
モデルの設定
RobynのdemoコードをベースにMMMを実行していきます。
サンプルデータを読み込みます。
また、各国の祝日情報を定義したデータを読み込みます。
library(Robyn) # サンプルデータの読み込み data("dt_simulated_weekly") # prophet用の祝日情報の読み込み data("dt_prophet_holidays")
はじめに入力変数の設定のオブジェクトを作成する必要がある。
かなりの要素を設定する必要があるようです。
## 入力変数の設定 InputCollect <- robyn_inputs( dt_input = dt_simulated_weekly, dt_holidays = dt_prophet_holidays, date_var = "DATE", # 日付変数の名前 記述形式は"2020-01-01"のようである必要がある dep_var = "revenue", # 従属変数の名前 dep_var_type = "revenue", # "revenue" (ROI) or "conversion" (CPA) を選択 prophet_vars = c("trend", "season", "holiday"), # 日次のデータには "all "を、週次以上のデータには "trend", "season", "holiday "を使うことを強く推奨 prophet_country = "DE", # 祝日情報を取り入れるために国の指定 context_vars = c("competitor_sales_B", "events"), # 競合他社、価格とプロモーション、気温、失業率など paid_media_spends = c("tv_S","ooh_S", "print_S" ,"facebook_S", "search_S"), # paid_media_varsで露出レベルの指標(インプレッション、クリック、GRPなど) paid_media_vars = c("tv_S", "ooh_S" , "print_S" ,"facebook_I" ,"search_clicks_P"), organic_vars = c("newsletter"), # ニュースレター配信、プッシュ通知、ソーシャルメディアへの投稿など factor_vars = c("events") ,# organic_vars あるいは context_vars で指定された変数のうち、どの変数が因子として強制されるべきかを指定する。 window_start = "2016-11-23",#モデリング期間の開始日と終了日 window_end = "2018-08-22", adstock = "geometric" # adstockの累積影響の形状をしているする、"geometric", "weibull_cdf", "weibull_pdf"のいずれか )
printすることで設定内容を確認できる。
> print(InputCollect) Total Observations: 208 (weeks) Input Table Columns (12): Date: DATE Dependent: revenue [revenue] Paid Media: tv_S, ooh_S, print_S, facebook_I, search_clicks_P Paid Media Spend: tv_S, ooh_S, print_S, facebook_S, search_S Context: competitor_sales_B, events Organic: newsletter Prophet (Auto-generated): trend, season, holiday on DE Unused: Date Range: 2015-11-23:2019-11-11 Model Window: 2016-11-21:2018-08-20 (92 weeks) With Calibration: FALSE Custom parameters: None Adstock: geometric Hyper-parameters: Not set yet
ハイパーパラメータの設定がまだされていないため、設定する。 hyper_names()を利用すると設定が必要なパラメータを確認できる。
## 設定すべきパラメータの確認 hyper_names(adstock = InputCollect$adstock, all_media = InputCollect$all_media)
なお、以下の関数でadstockのパラメータと形状の関係を視覚的に確認をすることができます。 パラメータの手助けになるとしています。
plot_adstock(plot = TRUE)
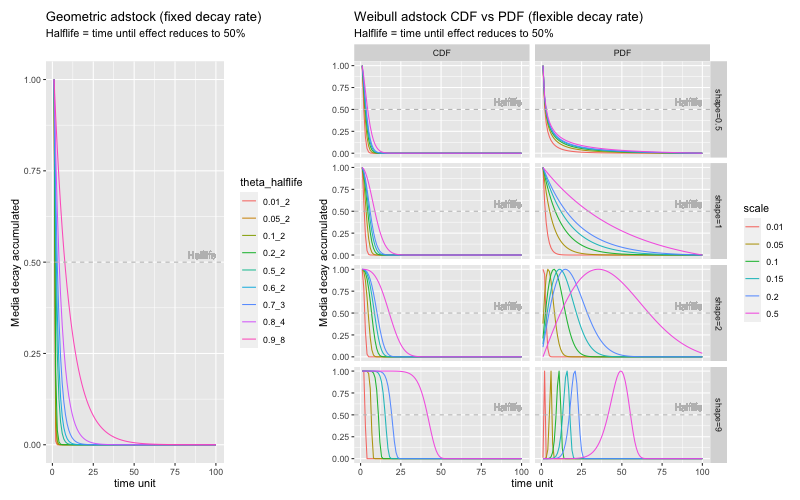
plot_saturation(plot = TRUE)
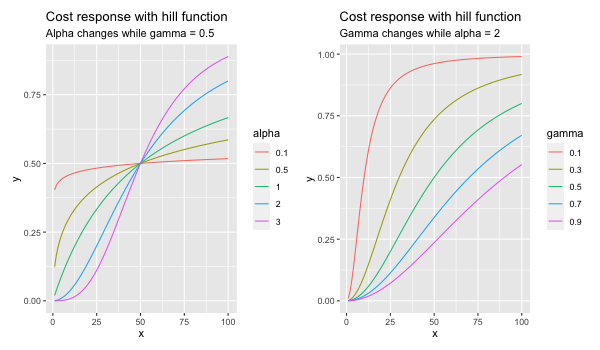
以下のようにパラメータごとの値域を設定。
hyperparameters <- list( facebook_S_alphas = c(0.5, 3), facebook_S_gammas = c(0.3, 1), facebook_S_thetas = c(0, 0.3), print_S_alphas = c(0.5, 3), print_S_gammas = c(0.3, 1), print_S_thetas = c(0.1, 0.4), tv_S_alphas = c(0.5, 3), tv_S_gammas = c(0.3, 1), tv_S_thetas = c(0.3, 0.8), search_S_alphas = c(0.5, 3), search_S_gammas = c(0.3, 1), search_S_thetas = c(0, 0.3), ooh_S_alphas = c(0.5, 3), ooh_S_gammas = c(0.3, 1), ooh_S_thetas = c(0.1, 0.4), newsletter_alphas = c(0.5, 3), newsletter_gammas = c(0.3, 1), newsletter_thetas = c(0.1, 0.4) )
モデルの推定
設定ができたのでモデルの実行をします。 adstockの設定をgeometricにすると比較的実行時間は短めですが、Weibull CDFやWeibull PDFを設定すると実行に時間がかかる模様
## モデル実行 InputCollect <- robyn_inputs(InputCollect = InputCollect, hyperparameters = hyperparameters) OutputModels <- robyn_run( InputCollect = InputCollect, iterations = 2000, trials = 5, outputs = FALSE )
結構時間がかかりますが、Stanモデルを自前で組みMCMCを実行するよりかは短いような気がします。 (手元のMBPで30分程度でした)
以下のように実行するとイテレーションを経るごとにモデルが収束している様子の確認することができる。
OutputModels$convergence$moo_distrb_plot
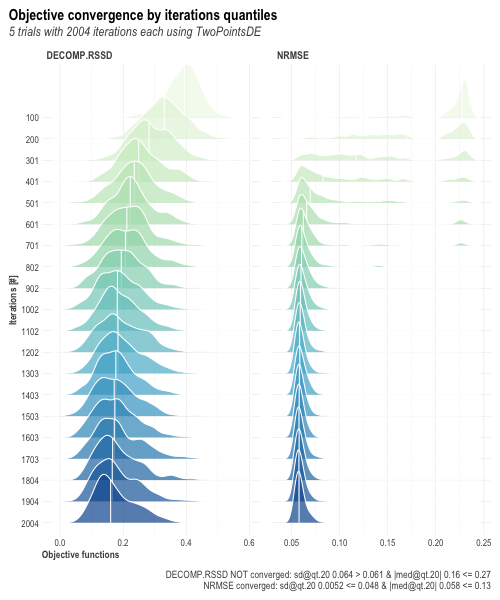
パレート最適な投資内容を抽出
投資効果を最大化するパラメータの組み合わせをもつモデルは複数存在する。
パレート最適なモデルを抽出し、分析することができる。
robyn_object <- "./MyRobyn.RDS" OutputCollect <- robyn_outputs( InputCollect, OutputModels, pareto_fronts = 3, csv_out = "pareto", # "pareto" or "all" clusters = TRUE, # TRUE:結果のクラスタリングを実行 plot_pareto = TRUE, # グラフのプロットの有無 plot_folder = robyn_object # 結果の出力先 )
結果を確認すると以下のようになる。
> print(OutputCollect) Plot Folder: ./2022-06-11 17.55 init/ Calibration Constraint: 0.1 Hyper-parameters fixed: FALSE Pareto-front (3) All solutions (170): 1_158_11, 1_166_2, 1_166_5, 2_114_4, 2_116_10, 2_126_11, 2_136_2, <略> Clusters (k = 4): 5_143_6, 2_147_4, 1_139_3, 3_151_7
1つのモデルを選択して保存します。
select_model <- "5_143_6" ExportedModel <- robyn_save( robyn_object = robyn_object, select_model = select_model, InputCollect = InputCollect, OutputCollect = OutputCollect, )
指定したモデルの推定されたパラメータを確認することができる。
> print(ExportedModel) Exported file: ./MyRobyn.RDS Exported model: 5_143_6 Media Summary for Selected Model: rn coef mean_spend mean_response roi_mean total_spend total_response roi_total 1: facebook_S 68410.32 136111.15 33104.02 0.2432131 5988890 1707974 0.2851903 2: ooh_S 202399.07 262577.85 88562.10 0.3372794 10240536 5763812 0.5628428 3: print_S 336224.55 77589.33 44599.30 0.5748123 2793216 2336391 0.8364521 4: search_S 102641.60 47618.18 29453.63 0.6185375 3666600 3221224 0.8785317 5: tv_S 434661.29 256198.38 128234.19 0.5005269 10247935 6904931 0.6737875
またこのモデルをグラフ化すると、以下のような情報を可視化することができる。
- 目的変数への影響度分解
- モデルのフィットの状況
- ROIとシェアについて
- 応答関数の形状
- 遅延率
- 残差
plot(ExportedModel)

アロケーションの最適化
推定したモデルを利用して投資組み合わせ(アロケーション)の最適化を行います。
AllocatorCollect1 <- robyn_allocator( InputCollect = InputCollect , OutputCollect = OutputCollect , select_model = select_model , scenario = "max_historical_response" , channel_constr_low = 0.7 , channel_constr_up = c(1.2, 1.5, 1.5, 1.5, 1.5) , export = TRUE , date_min = "2016-11-21" , date_max = "2018-08-20" )
結果を見ると、投資額の増減量とそれにより得られるリターン情報を確認することができます。
> print(AllocatorCollect1) Model ID: 5_143_6 Scenario: Maximum Historical Response Media Skipped (coef = 0): None Relative Spend Increase: 0% (+0) Total Response Increase (Optimized): 26.7% Window: 2016-11-21:2018-08-20 (92 weeks) Allocation Summary: - facebook_S: Optimizable Range (bounds): [-30%, 50%] Mean Spend Share (avg): 17.4% -> Optimized = 13% Mean Response: 33,104 -> Optimized = 23,608 Mean Spend (per time unit): 136.1K -> Optimized = 101K [Delta = -26%] - ooh_S: Optimizable Range (bounds): [-30%, 50%] Mean Spend Share (avg): 33.7% -> Optimized = 23.6% Mean Response: 88,562 -> Optimized = 77,071 Mean Spend (per time unit): 262.6K -> Optimized = 183.8K [Delta = -30%] - print_S: Optimizable Range (bounds): [-30%, 50%] Mean Spend Share (avg): 9.95% -> Optimized = 14.9% Mean Response: 44,599 -> Optimized = 105,596 Mean Spend (per time unit): 77.59K -> Optimized = 116.4K [Delta = 50%] - search_S: Optimizable Range (bounds): [-30%, 50%] Mean Spend Share (avg): 6.1% -> Optimized = 9.16% Mean Response: 29,454 -> Optimized = 48,696 Mean Spend (per time unit): 47.62K -> Optimized = 71.43K [Delta = 50%] - tv_S: Optimizable Range (bounds): [-30%, 20%] Mean Spend Share (avg): 32.8% -> Optimized = 39.4% Mean Response: 128,234 -> Optimized = 155,619 Mean Spend (per time unit): 256.2K -> Optimized = 307.4K [Delta = 20%]
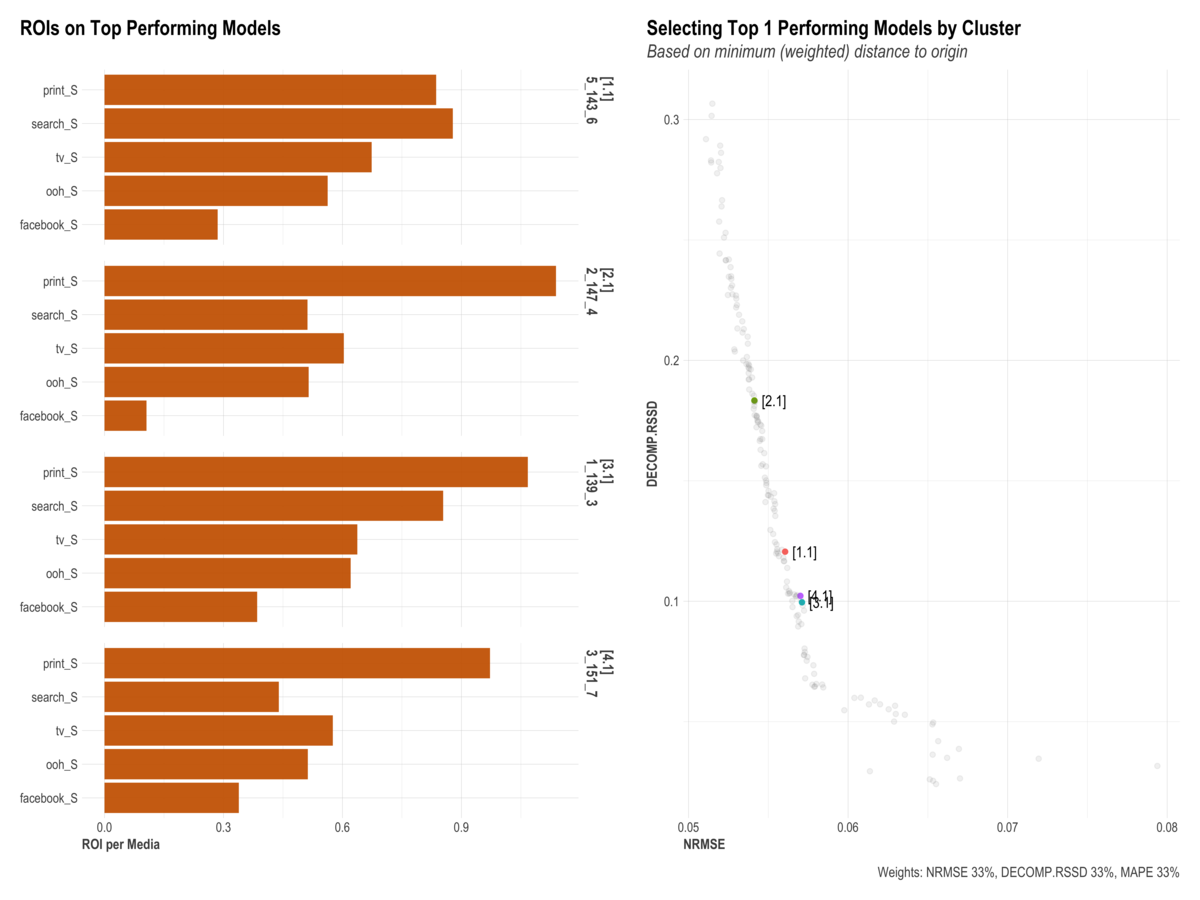
また、結果フォルダが生成され中に結果の情報をまとめたCSVやグラフが大量に生成されます。
その中には、最適なパラメータの組み合わせをk-meansによりクラスタリングした結果などが含まれる。 最適なクラスタ数の算出も行ってくれて今回はk=4であった。
投資額を設定したアロケーションの最適化
上記でシミュレーションしたモデルを利用し投資額上限を設定した7日間の最適化を行います。
AllocatorCollect2 <- robyn_allocator( InputCollect = InputCollect, OutputCollect = OutputCollect, select_model = select_model, scenario = "max_response_expected_spend", channel_constr_low = c(0.7, 0.7, 0.7, 0.7, 0.7), channel_constr_up = c(1.2, 1.5, 1.5, 1.5, 1.5), expected_spend = 1000000, # 投資上限 expected_spend_days = 7, # 最適化期間 export = TRUE )
こちらも投資の組み合わせの候補と結果を表示してくれます。
> print(AllocatorCollect2) Model ID: 5_143_6 Scenario: Maximum Response with Expected Spend Media Skipped (coef = 0): None Relative Spend Increase: 28.2% (+1.1M in 7 days) Total Response Increase (Optimized): 38.6% Window: 2016-11-21:2018-08-20 (92 weeks) Allocation Summary: - facebook_S: Optimizable Range (bounds): [-30%, 50%] Mean Spend Share (avg): 17.4% -> Optimized = 20.4% Mean Response: 33,104 -> Optimized = 46,010 Mean Spend (per time unit): 136.1K -> Optimized = 204.2K [Delta = 50%] - ooh_S: Optimizable Range (bounds): [-30%, 50%] Mean Spend Share (avg): 33.7% -> Optimized = 30.1% Mean Response: 88,562 -> Optimized = 93,023 Mean Spend (per time unit): 262.6K -> Optimized = 300.6K [Delta = 14%] - print_S: Optimizable Range (bounds): [-30%, 50%] Mean Spend Share (avg): 9.95% -> Optimized = 11.6% Mean Response: 44,599 -> Optimized = 105,596 Mean Spend (per time unit): 77.59K -> Optimized = 116.4K [Delta = 50%] - search_S: Optimizable Range (bounds): [-30%, 50%] Mean Spend Share (avg): 6.1% -> Optimized = 7.14% Mean Response: 29,454 -> Optimized = 48,696 Mean Spend (per time unit): 47.62K -> Optimized = 71.43K [Delta = 50%] - tv_S: Optimizable Range (bounds): [-30%, 20%] Mean Spend Share (avg): 32.8% -> Optimized = 30.7% Mean Response: 128,234 -> Optimized = 155,619 Mean Spend (per time unit): 256.2K -> Optimized = 307.4K [Delta = 20%]
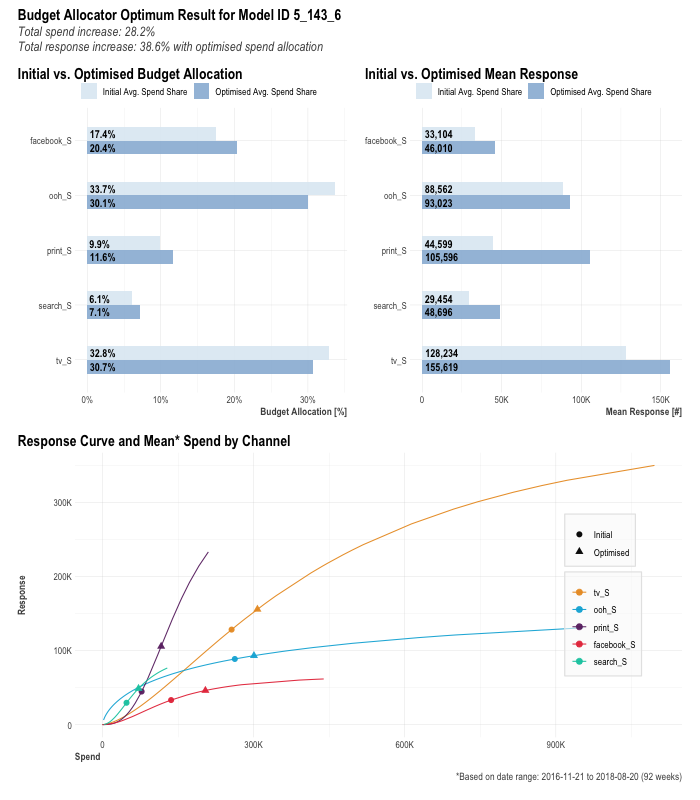
グラフ化すると基本的なシェア、レスポンス、応答関数の可視化が行えます。
plot(AllocatorCollect2)
所感
adstockの累積影響の形状など細かい設定を行うのは難しそうですが、非常に簡単にMMMを試すことができるのは嬉しいです。
特にアロケーションの最適化やそれらの結果の集計グラフ化を担ってくれる関数が揃っているのは非常にありがたいです。
実行内容をきちんと理解した上で利用できれば、かなり有用なライブラリではないでしょうか。 実践投入を行ってみたいですね。