はじめに
前から気になっていたこちらの書籍を読みました。
行間が怪しい部分も多かったですが、このシリーズらしく様々な要素を解説しているので、新しく知れる視点もありよかったです。
生存時間分析のモデルが、生存の予測を行う場合にはあまり力を発揮しない理由も自分なりに整理することができました。
その中でも比例ハザード性の確認についての部分は、一般的に非常に重要になるので簡単にまとめて起きたいと思います。
比例ハザード性について
生存時間分析では比例ハザードモデルを用いる場合が多いです。
比例ハザードモデルは説明変数がイベントまでの生存時間に影響を与えると考えるモデルです。
2つのハザード関数が、
に対して次のように関係式2つのハザード関数は比例する場合を考える。
ここで、は時間に寄らない比例定数である。
このような場合、あるハザード関数に対して、共変量
を条件づけた場合のハザード関数
を次のように表す。
ここで、はベースラインハザード (baseline hazard) と呼び、共変量が全て0の場合のハザード関数である。
係数からは、イベントの発生確率が
倍となるという情報が得られる。
この時、ハザード比は共変量のみに依存し、時間依存しないという比例ハザード性という仮定のもとに成り立つことを注意しなければならない。
library(survival) library(survminer) data("kidney") kidney_cox = coxph(Surv(time, status) ~ sex+age+disease+frail, data=kidney) summary(kidney_cox)
結果は以下の通りでした。
Call: coxph(formula = Surv(time, status) ~ sex + age + disease + frail, data = kidney) n= 76, number of events= 58 coef exp(coef) se(coef) z Pr(>|z|) sex -2.099844 0.122475 0.392654 -5.348 8.90e-08 *** age 0.007714 1.007744 0.011907 0.648 0.517055 diseaseGN 0.130666 1.139587 0.436114 0.300 0.764471 diseaseAN 0.640906 1.898200 0.447886 1.431 0.152442 diseasePKD -2.168515 0.114347 0.648825 -3.342 0.000831 *** frail 1.791873 6.000682 0.257639 6.955 3.53e-12 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 exp(coef) exp(-coef) lower .95 upper .95 sex 0.1225 8.1649 0.05673 0.2644 age 1.0077 0.9923 0.98450 1.0315 diseaseGN 1.1396 0.8775 0.48476 2.6790 diseaseAN 1.8982 0.5268 0.78904 4.5665 diseasePKD 0.1143 8.7453 0.03206 0.4079 frail 6.0007 0.1666 3.62158 9.9427 Concordance= 0.822 (se = 0.03 ) Likelihood ratio test= 68.71 on 6 df, p=8e-13 Wald test = 60.01 on 6 df, p=4e-11 Score (logrank) test = 86.24 on 6 df, p=<2e-16
比例ハザード性を満たしているかどうかは、書籍ではシェーンフィールド残差と時間が相関するかどうかで確認することができるとされている。 一方で比例ハザード性を満たしているかどうかの確認するの方法は、主に3つあるようです。
- 補対数-対数プロット
- Shoenfeld残差
- 時間依存性共変量
補対数-対数プロット
比例ハザードモデルの式を変換すると以下のようになる。

log(−logS(t))と時間tまたはlog(t)をプロットする。 共変量で決まる分ΣβX だけ切片が異なる平行な線が描かれる。 もし、比例ハザード性が成り立っているならば共変量によって層が異なる場合、プロットは平行になるはずである. 逆に、補対数対数プロットが並行でない場合は比例ハザード性の仮定が成立しないと言える。
並行かどうかについての判断は定量的に行うことはできず、主観で判断することになる。
Rでは以下のように確認できる。
性別で層化すると図のようになった。 並行であると言えば並行であると言えそうです。
plot(survfit(Surv(time, status) ~ sex, data=kidney), fun="cloglog", col=c("red", "blue"), lwd=2, xlab="log(Time)", ylab="log(-log S(t))")

シェーンフィールド残差について
シェーンフィールド残差についてはこちらの記事が分かりやすかったです。
Shoenfeld 残差は「ある時点 tiにおいて,イベントを起こした対象 i∈D の共変量 X_iξ とそうでない生存集団の共変量の期待値 A iξ (β) との差」ですが,もし比例ハザード仮定が成立するのであれば,「Shoenfeld 残差はイベントの発生した時間に関わらず,多少のばらつきはあってもおおよそ一定になっていそう」です.言い換えれば「Shoenfeld 残差がイベントの発生した時間に伴うなんらかの変化パターンをもっているような場合,比例ハザード仮定を破っていそう」ということになります.
そして、比例ハザード仮定が満たされているならShoenfeld残差は全イベント発生時点で合計するとゼロになり、時間によらず0周りに分布することになります。
このことを確認するには以下のようにする。
residuals_kidney_cox <- residuals(kidney_cox, type = "schoenfeld") cat(sum(residuals_kidney_cox)) # 9.354812e-11
全体のShoenfeld 残差はかなり0に近いようです。
それぞれの特徴量においても確認すると、0と言って良いようです。
> summary(residuals_kidney_cox) sex age diseaseGN diseaseAN diseasePKD frail Min. :-0.89116 Min. :-35.087 Min. :-0.6560 Min. :-0.5659 Min. :-0.45125 Min. :-1.90007 1st Qu.:-0.16030 1st Qu.: -9.277 1st Qu.:-0.2205 1st Qu.:-0.3276 1st Qu.:-0.09093 1st Qu.:-0.23951 Median : 0.08348 Median : 3.754 Median :-0.1376 Median :-0.1506 Median :-0.06104 Median : 0.04819 Mean : 0.00000 Mean : 0.000 Mean : 0.0000 Mean : 0.0000 Mean : 0.00000 Mean : 0.00000 3rd Qu.: 0.19180 3rd Qu.: 10.913 3rd Qu.: 0.0000 3rd Qu.: 0.4415 3rd Qu.:-0.02524 3rd Qu.: 0.25603 Max. : 0.87324 Max. : 24.692 Max. : 0.8991 Max. : 0.8939 Max. : 0.91367 Max. : 1.89409
ある変数についてSchoenfeld残差は時間と関連が認められなければ、その変数について比例ハザード性の仮定が成り立っているとなっている。
Schoenfeld残差は時間と関連を確認するのはSchoenfeld 残差検定である。
Rでは以下のように実施できる
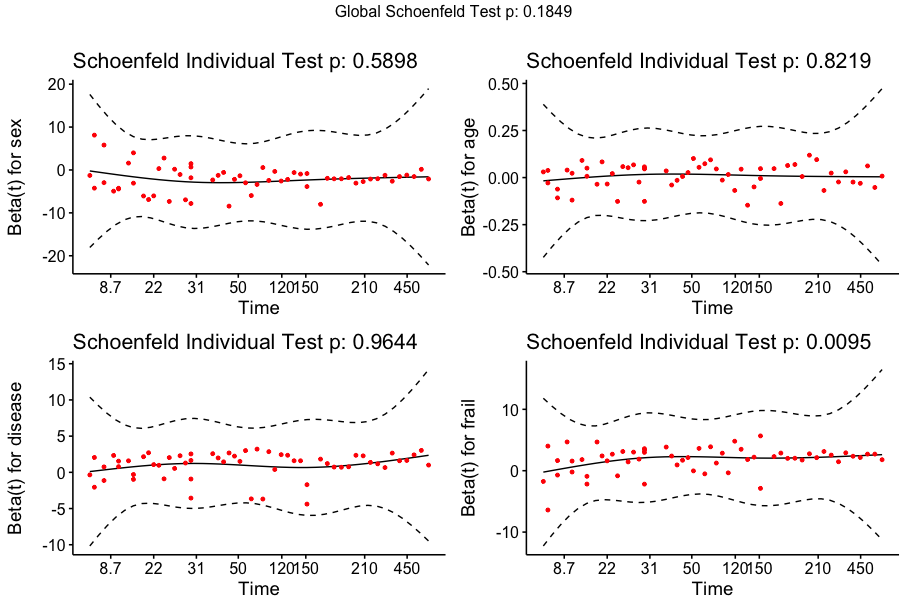
fit_test <- cox.zph(kidney_cox) ggcoxzph(fit_test) print(fit_test)
chisq df p sex 0.2907 1 0.5898 age 0.0507 1 0.8219 disease 0.2763 3 0.9644 frail 6.7193 1 0.0095 GLOBAL 8.8036 6 0.1849