はじめに

11月2日に行われた日本行動計量学会秋の行動計量セミナー「関数データ分析の基礎と使い方」に参加してきました。

昨年の統計関連学会連合大会で滋賀大学の松井先生の発表で関数データ分析という方法を知っていましたが、触れる機会はありませんでした。

そんな中、このセミナーの存在を知り、今後仕事で使えるかもしれないなという考えもあったため参加することにしました。

ここでは、そこで学んだこととRで実行する方法を簡単に(雑に)まとめたいと思います。

関数データ分析とは

日々の最高気温や関節軌道のように離散点で観測される(周期性のある)データには、背後にある滑らかな関数から生成されていると考えることができます。

その関数構造を抽出したデータが関数データです。

日々の最高気温の例では、一年間の最高気温の変化の関数が関数データとなります。

そのため関数データとは、観測データに順序のある多変量データであるとも言えます。

そして、関数データを使った関数データ分析では、各個体や対象に対して複数の離散点で時間や空間の変化に伴い観測・測定されたデータ(経時観測データ/空間データ)を関数の集合として捉え、解析する方法です。

関数データは、離散データを平滑化すること得られます。

１つの関数データは今までの統計的分析法の1変数と捉えると、様々な統計分析手法の関数データ分析が行うことができます。

記述統計量
関数主成分分析
関数回帰モデル・多変量関数回帰モデル
マルチレベルモデル
生存時間解析
判別，クラスタリング
検定
構造方程式モデル

関数データ分析の基本的な手順と種類

データを平滑化して，関数として分析に用いる事の利点としては、次のようなものが挙げられます。

どの地点（時点）でも値が評価可能となる
ノイズと構造を分離し，構造を分析できる
多時点（地点）観測データの高次元化による推定の不安定性を解決できる
曲線・局面の変化率が評価可能となる
時間・空間軸のレジストレーションが可能となる
多変量データ解析では困難な欠損へ対応可能
観測地点・個数のばらつきに対応可能
高次元データに典型的なノイズに対して頑健性があり、しかも効率的な計算が可能になる

Rではfdaパッケージで主要な関数データ分析は実行可能のようです。

関数データを作成する

観測しているデータの組を次のように表現します。

$\{(x_{\alpha i}, t_{\alpha i});i=1,2,\dots,N_{\alpha}, t_{\alpha i} \in T \} (\alpha = 1,2,\dots,n)$

また、関数の集合を次にように表現します。

$\{x_{\alpha}(t);\alpha=1,2,\dots,n, t \in T \} (\alpha = 1,2,\dots,n)$

このデータの組を関数で表現するために、平滑化を行います。よく用いられるのは基底展開による平滑化法です。 N 組の観測データが次の関数から生成されているとします。

$x_i = u(t_i)+\epsilon_i , i=1,2,\dots ,N$

ここで、分散 $\sigma ^2$ , 平均0の正規分布に従い、互い独立であるとする誤差です。この式に従うような滑らかな関数 $u_i (t)$ を求めることで、離散データを関数化することができます。

$u_i (t)$ の構造は、基底関数 $\phi_k(t)(k=1,2,\dots,m)$ の線形結合で表現できるとします。

$u(t)=\omega + \sum^m_{k=1} \omega_k \phi_k(t)$

この基底関数は様々なものが提案されており、次のようなものが代表的なものです。

フーリエ級数
ウェーブレット
B−スプライン
動径基底関数
Karhunen-Loeve展開
バーンスタイン基底関数

基底関数による平滑化

簡単に基底関数による平滑化(データの関数化)について説明します。

3次スプライン補間

説明変数 $t_i$ は区間 $[a,b$ ]上で次の様に並んでいるとします。

$a < t_1 < \dots < t_N < b$

ここで、説明変数 ${ t_1,\dots , t_N }$ を分割する $K(\leq N)$ 個の点であるノットを考えます。

$\tau_1<\dots<\tau_K$

各区分 $[a,\tau_1$ ,[a,\tau_1],\dots,[\tau_K,b]] 上のデータに対して1次式を当てはめたら１次スプラインです。 3次スプライン補間は、各区分のデータを3次式で補間する方法です。区分の接点では滑らかに繋ぐために、制約をつけた当てはめを行うことになります。

B-スプライン補間

B-スプラインは、複数の多項式を滑らかに接続した１つの基底関数を構成したものです。この時の基底関数は、r次B-スプライン基底関数と呼ばれます。

$b_k(t;r)$

3次スプライン補間では、まずn個のデータは(K-3)個の区間に分割します。

そして、B-スプライン基底関数は、各区間をr +1 個のr 次多項式からなることです。

例えば、3次B-スプライン関数は4つ(字数+1個)の3次多項式によって構成されているものになります。

このスプライン関数を用いて補間する方法が3次B-スプライン補間です。

観測データを3次B-スプライン基底関数の線形結合で近侍することにより、関数化することができます。

$x_i=\sum_{k=1}^K \omega_k b_k(t_i;3)+\epsilon_i, i=1,2, \dots , N$

関数データ回帰分析

関数データにおける回帰分析は、目的変数と説明変数のそれぞれでスカラー値と関数データを設定に応じてモデルも異なります。

目的変数＼説明変数	スカラー	関数データ
スカラー	一般的な回帰モデル	1
関数データ	2	3

1.スカラー-関数モデル

$i$ 番目の観測における説明変数のデータを $x_{it}$ ，目的変数のデータを $y_i$ とおくと関数線形モデルは次で与えられる。

$y_i=\beta_0+\int_T x_i(t)\beta_1 (t)dt+\epsilon_i$

説明変数 $x_{it}$ が𝑡の関数として与えられているためその係数𝛽𝑡も関数で与えられる

説明変数のデータ𝑥𝑖 𝑡 は，基底関数展開によって表されこの展開は，データの関数化によって得ることができるしたがって，ここでは係数𝒘𝑖 は既知とする

基底関数展開の仮定より，関数線形モデルは次のように変形できます。

\begin{align} y_i &= \beta_0+\int_T x_i(t)\beta_1 (t)dt+\epsilon_i \\\ &= \beta_0+w_i^T \int_T \phi(t) \phi(t)^T dt \gamma+\epsilon_i \\\ &= \beta_0+w_i^T \Phi \gamma+\epsilon_i \\\ &= \beta_0+z_i^T \gamma+\epsilon_i \end{align}

ここで、 $\Phi$ は交差積行列です。

$\Phi = \int_T \phi(t) \phi(t)^T dt$

𝒛𝑖は既知のため、このモデルは古典的な線形回帰モデルと同じ形とみなせることができます。

そのため、関数線形モデルでのパラメータは最小二乗法により推定することができます。

また、推定量の変動を抑えるために正則化を用いることが多い。

係数関数 $\beta_i$ も $x_{it}$ と同様，基底関数展開によって表されると仮定すると次のような関数形になります。

$\beta_i=\sum_{k=1}^m \gamma_k \phi_k (t)$

この時の基底関数𝜙𝑘 𝑡 の種類や数は𝑥𝑖 𝑡 のものと異なっていても大丈夫です。

そして、各点の信頼区間は次のように推定することができます。

通常の回帰分析の場合と同様に、説明変数を増やす重回帰分析も行うことができる。

$y_i=\beta_0+\sum \int_T x_i(t)\beta_1 (t)dt+\epsilon_i$

なお、通常の重回帰モデルと同様にスパース推定等の方法を用いると変数選択も行うことができる。

一般化線形モデルへの拡張も可能である。

2.関数-スカラーモデル

説明変数と目的変数が共に関数データで与えられたモデルです。

説明変数のデータを𝑥𝑖，目的変数のデータを𝑦𝑖 𝑡 とおくと関数線形モデルは次で与えられるます。

$y_i(t)=x_i\beta_1 (t)+\epsilon_i(t)$

スカラー-関数型線形モデルと同様の形で， $y_i(t)$ は基底関数展開によって表されると仮定しています。

$y_i(t)=\sum_{l=1}^{m} v_{il}\phi_l (t)$

$\beta_t$ も基底関数展開によって表されると仮定すると次のように表現できます。

$\beta_1(t)=\sum_{l=1}^{m} b_{l}\phi_l (t)$

3.関数-関数モデル

説明変数と目的変数が共に関数データで与えられたモデルです。

$y_i(t)=\int_{T} x_i(s)\beta_1 (s, t) ds+\epsilon_i(t)$

ここでsとtの間隔は異なっても良いです. 例えば、毎時と毎日の単位で計測されたデータのようなものが挙げられます。

Rで関数データ回帰分析

ここでは気温データを関数データとして、年間降水量を回帰する分析を行います。

用いるデータはfdaパッケージに含まれるカナダの36地点の1960~1994年の平均基本のデータです。

はじめにデータを可視化してみます。

library(tidyverse)
library(fda)

data(daily)

# 日本語設定
par(family = "HiraKakuProN-W3")

matplot(daily$tempav, type="l", main="日別平均気温")

当たり前ですが、夏場に気温が高くて冬場に気温が低いですね。

次に気温データを関数データにします。

temp_basis <- create.fourier.basis(c(0,365), 65) #基底関数を構築
temp_Smooth <- smooth.basis(day.5, daily$tempav, temp_basis) #関数化
tempfd <- temp_Smooth$fd
plot(tempfd, main="関数データ")

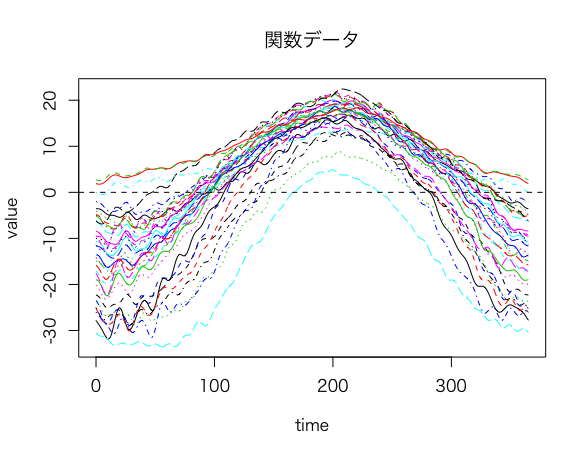
関数回帰分析を実行します。

# 関数化した説明変数を形成
temp_list <- vector("list", 2)
temp_list[[1]] <- rep(1,35)  #定数項
temp_list[[2]] <- tempfd     #気温データ（関数化済）

# 係数情報を形成
con_basis <- create.constant.basis(c(0,365))  #定数項
beta_basis <- create.fourier.basis(c(0,365),5)  #係数関数の基底関数
beta_list <- vector("list",2)
beta_list[[1]] <- con_basis
beta_list[[2]] <- beta_basis

# 関数回帰分析を実行
FR_model <- fRegress(annualprec,temp_list,beta_list)

# 係数関数を出力
betaestlist <- FR_model$betaestlist
tempbetafd <- betaestlist[[2]]$fd
plot(tempbetafd, xlab="Day", ylab="Beta for temperature")

f:id:saltcooky:20191201192134p:plain — 係数関数

春から初夏と冬場は、降水量に対して気温は正の影響、それ以外の時期は負の影響があると考えられます。

次に、推定される係数関数に対して正則化を行なった場合の関数回帰分析を行なってみたいと思います。

# 正則化項構築
Lcoef = c(0,(2*pi/365)^2,0)
harmaccelLfd = vec2Lfd(Lcoef, c(0,365))  # 差分作用素（非負定値行列に対応）
betabasis = create.fourier.basis(c(0, 365), 35)  # 係数関数の基底関数
lambda = 10^12.5  # 正則化パラメータ
betafdPar = fdPar(betabasis, harmaccelLfd, lambda)  #関数回帰モデルのパラメータ集合
beta_list[[2]] = betafdPar

# 関数回帰実行
fRegressList = fRegress(annualprec,temp_list,beta_list)

# 係数関数出力
betaestlist = fRegressList$betaestlist
tempbetafd = betaestlist[[2]]$fd
plot(tempbetafd, xlab="Day", ylab="Beta for temperature")

f:id:saltcooky:20191210014138p:plain

冬場以外は気温に対する降水量の影響は存在していないと言えそうです。これは、降水量には降雪も含まれており、カナダという土地柄気温が下がり降雪が多くことが起こる冬のみ影響があるといえるの可能性があります。

関数データ主成分分析

(かなり雑ですよ。)

通常の主成分分析では、分散共分散行列を計算して固有値を求めます。

一方で、関数データでの主成分分析では、分散共分散行列を算出することはできないため、代わりに共分散作用素を用いた固有値問題を考えます。

確率過程における共分散関数(covariance function)は、次式で表現されます。

$K(s,t) = Cov(X(s),X(t))$

確率過程の共分散作用素(covariance operator) $H$ は、次の式を満たすものとなります。

$(Hf)(t)=\int K(t,s)f(s)ds$

共分散作用素Hを推定値 $V$ は次式により表現されます。

$(Vf)(t)=\int v(t,s)f(s)ds$

ここで $v(s,t)$ は、標本共分散関数です。

$v(t,s) = \frac{1}{n} \sum_{i=1}^n x_i(s) x_i(t)$

主成分得点は、データと重み関数の内積で求められるスコアの分散となります。

$f_i=<\beta,x_i>=\int \beta(s) x_i (s)ds, i=1,...,n$

そして、多変量データに対するPCAと同様に、データの情報を多く含む=ばらつきが大きい成分である主成分得点 $f_i$ を抽出することを考えます。実際には、次の最大化問題を考えます。

$\hat \beta=argmax_{\beta} Var_n(f) \quad s.t. \| \beta \| =1$

この時、次の等式が成立し、分散最大化問題は作用素 $V$ の固有値問題に帰着します。

$Var_n(f)=< \beta , V \beta>$

主成分得点の分散 $Var_n(f)$ の最大値を与える主成分ベクトル $\beta$ は，共分散作用素 $V$ の最大固有値に対応する固有ベクトルとなります。

Rで関数データ主成分分析

fdaパッケージには歩行時の膝関節と股関節の角度変化のデータgaitが含まれています。ここでは、そのうちの膝関節の角度データについて関数データ主成分分析を実行します。はじめにデータの可視化を行なってみます。

knee_df <- gait[,,2]

N.knee <- dim(knee_df)[1] 
point_time <- rownames(knee_df)

matplot(point_time, 
        knee_df, 
        type="l", 
        xlab = "time", 
        ylab = "knee angle", 
        lwd = 1)

では、このデータに対して関数主成分分析を行います。

# B-spline基底を定義
curv_Lfd <- int2Lfd(2) # 2は微分作用素の次数

# fdParオブジェクトを定義
curv_fdPar <- fdPar(bbasis, curv_Lfd, 0)

lambdas <- 10^seq(-4,4,by=0.5) # lambdaの候補を設定
len_lambdas <- length(lambdas)
mean_gcv <- rep(0,len_lambdas)
for(n_lambda in 1:len_lambdas){
  print(n_lambda)
  curv_fdPari <- curv_fdPar
  curv_fdPari$lambda <- lambdas[n_lambda]
  
 # 平滑化
  temp_smooth.i <- smooth.basis(dtime, knee_df, curv_fdPari) 
  
  mean_gcv[n_lambda] <- mean(temp_smooth.i$gcv)
}

best <- which.min(mean_gcv)
lambdabest <- lambdas[best]

curv_fdPar$lambda <- lambdabest
temp_smooth <- smooth.basis(dtime, knee_df, curv_fdPar)
temp_fd <- temp_smooth$fd

# 関数主成分分析の実行 
res.fpca <- pca.fd(temp_fd, nharm=Norder)